前言

时间终于来到了2017年，我的文章也终于要追上3GPP 5G NR标准化的进展了。自2016年11月3GPP RAN1 #87会议确定5G eMBB场景控制信道编码为Polar Code后，2017年1月在美国斯波坎市召开的3GPP RAN1 #AH1_NR会议上继续讨论了Polar Code设计议题。紧接着，2月（上个月）在希腊雅典召开了RAN1 #88次会议；3月（本月）在克罗地亚召开了RAN #75次全会，5G的研究阶段（Study Item，SI）结束，继而开启工作阶段（Work Item）；4月（下个月）3日又将在美国召开RAN1 #88b会议。5G的推进速度其实比外界想象得要快得多。

前言

Arikan发明极化码时给出了编码算法和SC译码算法，后来的研究者提出SCL和CA-SCL译码算法对SC算法进行了改进，使译码性能得到提升。但不要忘记这些编译码算法都对码长有限定条件，即码长必须满足2的幂次方：\(N={ {2}^{n}}\)。虽然当码长\(N\)固定时，信息比特长度\(K\)可以任意取值，编码速率\(R={K}/{N}\;\)也能随之自由变化。但在信息比特长度一定的情况下，要通过调整码长而调整编码速率就无法实现了。从实际角度出发，我们更希望设计一对编译码器能够在不改变基本的编译码结构的情况下，使码长和编码速率都能够自适应调节。在设计速率可变的编码时，凿孔是一种普遍采用的方法。

前言

循环冗余校验（Cyclic redundancy check，CRC）是一种信道检错技术，在实际数字通信系统中已经得到了广泛应用。对于Polar码而言，在SCL译码结束时得到一组候选路径，能够以非常低的复杂度与CRC进行联合检测译码，选择能够通过CRC检测的候选序列作为译码器输出序列，从而提高译码算法的纠错能力。

CA-SCL译码算法

文献[1]提出了CRC辅助的SCL（CRC-aided SCL，CA-SCL）译码算法，在信息比特序列中添加CRC校验比特序列，利用SCL译码算法正常译码获得\(L\)条搜索路径，然后借助“正确信息比特可以通过CRC校验”的先验信息，对这\(L\)条搜索路径进行挑选，从而输出最佳译码路径。给定Polar码码长为\(N\)，CRC校验码码长为\(m\)，若极化码的信息为长度为\(K\)，编码信息比特的长度为\(k\)，如图1所示，有\(K=k+m\)。Polar码的码率仍然为\(R={K}/{N}\;\)。

前言

通过系列文章《Polar Code（1~7）》大致梳理了Polar Code从编码到译码的基本原理和算法步骤。本文回过头再来谈一谈高斯近似。高斯近似已在前文《Polar Code（4）编码之极化信道可靠性估计》中有所介绍。对于Polar码的研究从BEC到一般类型的B-DMC，再到BAWGNC，越来越从理想走向实际。密度进化法把BEC扩展到了所有类型的B-DMC，高斯近似法则把B-DMC再次扩展到了BAWGNC。本文将梳理高斯近似在Polar Code编码和译码中的具体应用。

前言

Polar Code在码长趋于无穷时，信道极化才越完全。但在有限码长下，由于信道极化并不完全，依然会存在一些信息比特无法被正确译码。当前面\(i-1\)个信息比特的译码中发生错误之后，由于SC译码器在对后面的信息比特译码时需要用到之前的信息比特的估计值，这就会导致较为严重的错误传递。SC译码算法是一种贪婪算法，对码树的每一层仅仅搜索到最优路径就进行下一层，所以无法对错误进行修改。SCL译码算法就是对SC算法的改进。但在SCL之前，先来看看SC译码算法的码树表示。

前言

Arikan在文献[1]中给出了Polar Code译码算法，即串行抵消（Successive Cancellation，SL）译码算法。由Polar Code编码原理可知，极化码的构造就是一个极化信道的选择问题，而极化信道的选择实际上是按照最优化SC译码性能为标准的。根据极化信道转移概率函数式，各个极化信道并不是相互独立的，而是具有确定的依赖关系的：信道序号大的极化信道依赖于所有比其序号小的极化信道。基于极化信道之间的这一依赖关系，SC译码算法对各个比特进行译码判决时，需要假设之前步骤的译码得到的结果都是正确的。并且正是在这种译码算法下，极化码被证明了是信道容量可达的。因此对极化码而言，最合适的译码算法应当是基于SC译码的，只有这类译码算法才能充分利用极化码的结构，并且同时保证在码长足够长时容量可达。

前言

极化信道的可靠性估计是Polar Code编码的第一步，对于BEC信道，若计算巴氏参数，转移概率是绕不开的一步。此外对于译码判决来说，计算转移概率也是必须的。本文就尝试梳理一下极化信道的转移概率\(W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}} \right)\)。

离散信道的数学模型

信道是信号传输的媒介，是传送信息的通道。在信息论研究中不考虑信道的物理特性，而只是考虑它的概率特性。研究信道的目的主要是为了解决信息如何通过信道实现有效和可靠传输的问题。香农第二定理指出，信息传输速率小于信道容量是实现可靠传输的充分与必要的条件。信道容量是信息能够可靠传输的最大信息传输速率，是信道研究中的一个重要内容。信道容量定义为信道输入与输出平均互信息的最大值，它是信道本身固有特性的反映，仅与信道的转移概率有关，与信道的输入概率无关，但是信道输人概率必须与信道匹配才能达到容量。

《Polar Code（4）编码之极化信道可靠性估计》提到，事件\({ {A}_{i}}\)表示序号为\(i\)的极化信道\(W_{N}^{\left( i \right)}\)所承载的比特经过传输后接收发生错误，即

\[ { {A}_{i}}=\left\{ u_{1}^{N},y_{1}^{N}:W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}} \right)<W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}}\oplus 1 \right) \right\} \]

则极化信道\(W_{N}^{\left( i \right)}\)的错误概率为\(P\left( { {A}_{i}} \right)\)。

那么事件\({ {A}_{i}}\)怎么理解？

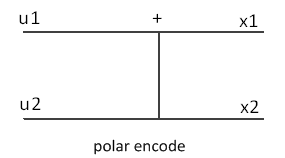
举个例子，假设N=2。编码器输入是\(\left( \begin{matrix} { {u}_{1}} \\ { {u}_{2}} \\ \end{matrix} \right)\)，编码器输出是\(\left( \begin{matrix} { {x}_{1}}={ {u}_{1}}\oplus { {u}_{2}} \\ { {x}_{2}}={ {u}_{2}} \\ \end{matrix} \right)\)。经过无线信道，假设接收端接收到的信号为\(y_{1}^{2}\)。

前言

由Arikan发明的Polar Code经典编码算法已在《Polar Code（2）编码原理》中阐明，《Polar Code（3）编码实例》则是对前文的举例。在编码实例中，有两个前提假设：

1. 假设一个二进制删除信道（BEC）；
2. 假设采用计算巴氏参数来评估各分裂子信道的可靠性。

Arikan在讨论信道极化时，针对的是二进制离散无记忆信道（B-DMC），然而在构造极化码时需要计算的巴氏参数\(Z\left( W \right)\)的适用范围是二进制删除信道。BEC是B-DMC的子集。因此在Polar Code编码时只能回落的BEC来进行构造。

前言

在《Polar Code（2）编码原理》中详细阐述了Polar Code编码原理，为更好地理解编码过程，本文将给出一个编码实例。

设码长为\(N=8\)，消息比特数\(K=4\)。列出所有使用到的公式：

\[c_{1}^{N}=u_{1}^{N}{G_{N}}\]

\[{G_{N}}={B_{N}}{F^{\otimes n}}\]