Polar Code（6）SC译码算法

发表于 2017-03-13 更新于 2018-10-21 分类于 Polar Code 阅读次数：

前言

Arikan在文献[1]中给出了Polar Code译码算法，即串行抵消（Successive Cancellation，SL）译码算法。由Polar Code编码原理可知，极化码的构造就是一个极化信道的选择问题，而极化信道的选择实际上是按照最优化SC译码性能为标准的。根据极化信道转移概率函数式，各个极化信道并不是相互独立的，而是具有确定的依赖关系的：信道序号大的极化信道依赖于所有比其序号小的极化信道。基于极化信道之间的这一依赖关系，SC译码算法对各个比特进行译码判决时，需要假设之前步骤的译码得到的结果都是正确的。并且正是在这种译码算法下，极化码被证明了是信道容量可达的。因此对极化码而言，最合适的译码算法应当是基于SC译码的，只有这类译码算法才能充分利用极化码的结构，并且同时保证在码长足够长时容量可达。

SC译码算法

在进行译码时，从式（1）的转移概率可以看出，序号$i$极化信道$W_{N}^{\left( i \right)}$的输出包括信道接收信号$y_{1}^{N}$以及前$i-1$个极化信道的输入$u_{1}^{i-1}$两个部分。

\[\begin{align} W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}} \right)\triangleq \sum\limits_{u_{i+1}^{N}\in { {X}^{N-i}}}{\frac{1}{ { {2}^{N-1}}}{ {W}_{N}}\left( y_{1}^{N}|u_{1}^{N} \right)} \end{align}\]

因此，对于$i\in \left\{ 1,2,...,N \right\}$，比特${ {u}_{i}}$的估计值${ {\hat{u}}_{i}}$可以根据接收信号$y_{1}^{N}$和部分估计序列$u_{1}^{i-1}$通过计算当${ {\hat{u}}_{i}}=0$或${ {\hat{u}}_{i}}=1$时$W_{N}^{\left( i \right)}$的转移概率进行逐个地判断。这种译码算法称为串行抵消（SC）译码算法：对信道序号$i$从1到N取值，各个比特的估计值根据以下公式得到：

\[\begin{align} { {\hat{u}}_{i}}=\left\{ \begin{matrix} { {h}_{i}}\left( y_{1}^{N},\hat{u}_{1}^{i-1} \right),\ \ if\ i\in A \\ { {u}_{i}},\ \ if\ i\in { {A}^{c}} \\ \end{matrix} \right. \end{align}\]

其中，当$i\in { {A}^{c}}$时，表明该比特为冻结比特，即收发端事先约定的比特，因此直接判决为${ {\hat{u}}_{i}}={ {u}_{i}}$；当$i\in A$时，表明该比特为承载信息的信息比特，判决函数为

\[\begin{align} { {h}_{i}}\left( y_{1}^{N},\hat{u}_{1}^{i-1} \right)=\left\{ \begin{matrix} 0,\ \ if\ L_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1} \right)\ge 0 \\ 1,\ \ if\ L_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1} \right)<0\ \\ \end{matrix} \right. \end{align}\]

定义对数似然比（Log-Likelihood Ratio，LLR）为

\[\begin{align} L_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1} \right)\triangleq \ln \left( \frac{W_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1}|0 \right)}{W_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1}|1 \right)} \right) \end{align}\]

LLR的计算可以通过递归完成。现定义函数$f$和$g$如下：

\[\begin{align} f\left( a,b \right)=\ln \left( \frac{1+{ {e}^{a+b}}}{ { {e}^{a}}+{ {e}^{b}}} \right) \end{align}\]

\[\begin{align} g\left( a,b,{ {u}_{s}} \right)={ {\left( -1 \right)}^{ { {u}_{s}}}}a+b \end{align}\]

其中，$a,b\in R,{ {u}_{s}}\in \left\{ 0,1 \right\}$。LLR的递归运算借助函数$f$和$g$表示如下：

\[\begin{align} L_{N}^{\left( 2i-1 \right)}\left( y_{1}^{N},\hat{u}_{1}^{2i-2} \right)=f\left( L_{N/2}^{\left( i \right)}\left( y_{1}^{ {N}/{2}\;},\hat{u}_{1,o}^{2i-2}\oplus \hat{u}_{1,e}^{2i-2} \right),L_{N/2}^{\left( i \right)}\left( y_{ {N}/{2}\;+1}^{N},\hat{u}_{1,e}^{2i-2} \right) \right) \end{align}\]

\[\begin{align} L_{N}^{\left( 2i \right)}\left( y_{1}^{N},\hat{u}_{1}^{2i-1} \right)=g\left( L_{N/2}^{\left( i \right)}\left( y_{1}^{ {N}/{2}\;},\hat{u}_{1,o}^{2i-2}\oplus \hat{u}_{1,e}^{2i-2} \right),L_{N/2}^{\left( i \right)}\left( y_{ {N}/{2}\;+1}^{N},\hat{u}_{1,e}^{2i-2} \right),{ { {\hat{u}}}_{2i-1}} \right) \end{align}\]

递归的终止条件为当$N=1$时，即到达了信道$W$端，此时$L_{1}^{\left( 1 \right)}\left( { {y}_{j}} \right)=\ln \frac{W\left( { {y}_{j}}|0 \right)}{W\left( { {y}_{j}}|1 \right)}$。

定义事件“SC译码算法得到的译码码块错误”为$E=\bigcup\nolimits_{i=1}^{N}{ { {B}_{i}}}$，其中事件

\[\begin{align} { {B}_{i}}=\left\{ u_{1}^{N},y_{1}^{N}:u_{1}^{i-1}=\hat{u}_{1}^{i-1},W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}} \right)<W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}}\oplus 1 \right) \right\} \end{align}\]

表示“SC译码过程中第一个错误判决发生在第$i$个比特”。由于${ {B}_{i}}\subset { {A}_{i}}$（事件${ {A}_{i}}$的定义参看《Polar Code（4）编码之极化信道可靠性估计》前言），因此有$E\subset \sum\limits_{i\in A}{P\left( { {A}_{i}} \right)}$，于是

\[\begin{align} P\left( E \right)\le \sum\nolimits_{i\in A}{P\left( { {A}_{i}} \right)} \end{align}\]

其中$P\left( { {A}_{i}} \right)$的值可根据前文所述的计算巴氏参数、密度进化或高斯近似方法得到。因此，通过式（6）可以得到极化码在SC译码下的误块率（BLER）性能上界。

$L_{1}^{\left( 1 \right)}\left( { {y}_{j}} \right)=\ln \frac{W\left( { {y}_{j}}|0 \right)}{W\left( { {y}_{j}}|1 \right)}$在这里仍属于定义式，在实际中并不具有操作性，因为转移概率$W$是未知的。当引入高斯近似法，接收符号$y$的对数似然比（LLR）定义为

\[L\left( y \right)=\ln \frac{p\left( y|0 \right)}{p\left( y|1 \right)}=\frac{2y}{ { {\sigma }^{2}}}\]

因此译码端对数似然比的初始值$L_{1}^{\left( 1 \right)}\left( { {y}_{j}} \right)=\frac{2y}{ { {\sigma }^{2}}}$可轻松获得，$y$为接收符号，${ {\sigma }^{2}}$为噪声方差。

SC译码示例

现在以码长$N=4$，消息比特数为$K=3$的极化码为例，对SC译码进行说明。在图1中，${ {u}_{1}}$为冻结比特并设定为零值，而消息比特也假设为全零，最右端的$L_{1}^{\left( 1 \right)}\left( { {y}_{j}} \right)$表示接收自信道的对数似然比。其他节点表示中间估计结果以及中间译码结果。

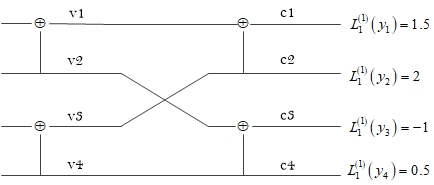
图 1 极化码的SC译码，初始状态

需要说明的是，编码过程中计算转移概率是从图的左边逐级向右边递归。而在译码过程中，计算信道的LLR要从右边逐级向左递归。

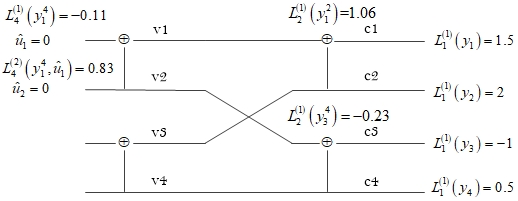
SC译码算法将首先计算${ {u}_{1}}$的对数似然比$L_{4}^{\left( 1 \right)}\left( y_{1}^{4} \right)$。根据式（5）和式（7），如图2所示，首先计算出$L_{2}^{\left( 1 \right)}\left( y_{1}^{2} \right)$和$L_{2}^{\left( 1 \right)}\left( y_{3}^{4} \right)$的值，其中

\[\begin{align} L_{2}^{\left( 1 \right)}\left( y_{1}^{2} \right)=f\left( L_{1}^{\left( 1 \right)}\left( { {y}_{1}} \right),L_{1}^{\left( 1 \right)}\left( { {y}_{2}} \right) \right)\text{=}\ln \left( \frac{1+{ {e}^{1.5+2}}}{ { {e}^{1.5}}+{ {e}^{2}}} \right)=1.06 \end{align}\]

\[\begin{align} L_{2}^{\left( 1 \right)}\left( y_{3}^{4} \right)=f\left( L_{1}^{\left( 1 \right)}\left( { {y}_{3}} \right),L_{1}^{\left( 1 \right)}\left( { {y}_{4}} \right) \right)\text{=}\ln \left( \frac{1+{ {e}^{-1+0.5}}}{ { {e}^{-1}}+{ {e}^{0.5}}} \right)=-0.23 \end{align}\]

接着计算出$L_{4}^{\left( 1 \right)}\left( y_{1}^{4} \right)$：

\[\begin{align} L_{4}^{\left( 1 \right)}\left( y_{1}^{4} \right)=f\left( L_{2}^{\left( 1 \right)}\left( y_{1}^{2} \right),L_{2}^{\left( 1 \right)}\left( y_{3}^{4} \right) \right)=\ln \left( \frac{1+{ {e}^{1.06-0.23}}}{ { {e}^{1.06}}+{ {e}^{-0.23}}} \right)=-0.11 \end{align}\]

虽然$L_{4}^{\left( 1 \right)}\left( y_{1}^{4} \right)<0$，但由于${ {u}_{1}}$是冻结比特，我们依然将${ {u}_{1}}$判决为${ {\hat{u}}_{1}}=0$。

$图 2 极化码的SC译码，对${ {u}_{1}}$译码$

接着对${ {u}_{2}}$进行译码，如图3所示，根据式（6）和式（8）可得

\[\begin{align} L_{4}^{\left( 2 \right)}\left( y_{1}^{4},{ { {\hat{u}}}_{1}} \right)={ {\left( -1 \right)}^{ { { {\hat{u}}}_{1}}}}L_{2}^{\left( 1 \right)}\left( y_{1}^{2} \right)+L_{2}^{\left( 1 \right)}\left( y_{3}^{4} \right)={ {\left( -1 \right)}^{0}}\times 1.06+\left( -0.23 \right)=0.83 \end{align}\]

由于${ {u}_{2}}$是消息比特且$L_{4}^{\left( 2 \right)}\left( y_{1}^{4},{ { {\hat{u}}}_{1}} \right)>0$，因此判决为${ {\hat{u}}_{2}}=0$，此处为正确译码。

$图 3 极化码的SC译码，对${ {u}_{2}}$译码$

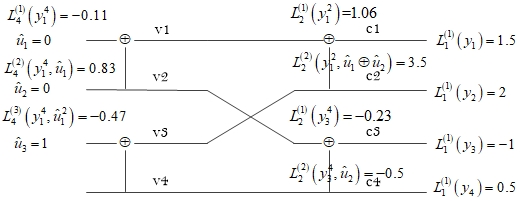
接着对${ {u}_{3}}$进行译码，如图4所示，根据式（5）和式（7）可得

\[\begin{align} L_{4}^{\left( 3 \right)}\left( y_{1}^{4},\hat{u}_{1}^{2} \right)=f\left( L_{2}^{\left( 2 \right)}\left( y_{1}^{2},{ { {\hat{u}}}_{1}}\oplus { { {\hat{u}}}_{2}} \right),L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ { {\hat{u}}}_{2}} \right) \right) \end{align}\]

这里需要先求$L_{2}^{\left( 2 \right)}\left( y_{1}^{2},{ { {\hat{u}}}_{1}}\oplus { { {\hat{u}}}_{2}} \right)$，根据式（6）和式（8）可得

\[\begin{align} L_{2}^{\left( 2 \right)}\left( y_{1}^{2},{ { {\hat{u}}}_{1}}\oplus { { {\hat{u}}}_{2}} \right)={ {\left( -1 \right)}^{ { { {\hat{u}}}_{1}}\oplus { { {\hat{u}}}_{2}}}}L_{1}^{\left( 1 \right)}\left( { {y}_{1}} \right)+L_{1}^{\left( 1 \right)}\left( { {y}_{2}} \right)={ {\left( -1 \right)}^{0}}\times 1.5+2=3.5 \end{align}\]

再求$L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ { {\hat{u}}}_{2}} \right)$，根据根据式（6）和式（8）可得

\[\begin{align} L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ { {\hat{u}}}_{2}} \right)\text{=}{ {\left( -1 \right)}^{ { { {\hat{u}}}_{2}}}}L_{1}^{\left( 1 \right)}\left( { {y}_{3}} \right)+L_{1}^{\left( 1 \right)}\left( { {y}_{4}} \right)={ {\left( -1 \right)}^{0}}\times \left( -1 \right)+0.5=-0.5 \end{align}\]

把式（16）和式（17）带入到式（15）得到

\[\begin{align} L_{4}^{\left( 3 \right)}\left( y_{1}^{4},\hat{u}_{1}^{2} \right)=f\left( 3.5,-0.5 \right)\text{=}\ln \left( \frac{1+{ {e}^{3.5-0.5}}}{ { {e}^{3.5}}+{ {e}^{-0.5}}} \right)=-0.47 \end{align}\]

由于$L_{4}^{\left( 3 \right)}\left( y_{1}^{4},\hat{u}_{1}^{2} \right)<0$，因此判决${ {\hat{u}}_{3}}=1$，此处发生译码错误。

$图 4 极化码的SC译码，对${ {u}_{3}}$译码$

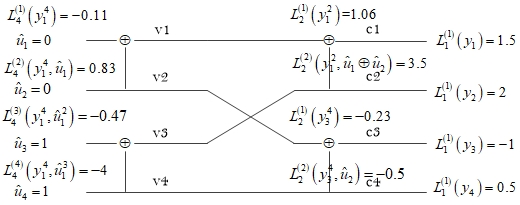
最后对${ {u}_{4}}$进行译码，如图5所示，根据式（6）和式（8）可得

\[\begin{align} \nonumber & L_{4}^{\left( 4 \right)}\left( y_{1}^{4},\hat{u}_{1}^{3} \right)={ {\left( -1 \right)}^{ { { {\hat{u}}}_{3}}}}L_{2}^{\left( 2 \right)}\left( y_{1}^{2},{ { {\hat{u}}}_{1}}\oplus { { {\hat{u}}}_{2}} \right)+L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ { {\hat{u}}}_{2}} \right) \\ \nonumber & ={ {\left( -1 \right)}^{1}}\times 3.5+\left( -0.5 \right) \\ & =-4 \\ \end{align}\]

由于$L_{4}^{\left( 4 \right)}\left( y_{1}^{4},\hat{u}_{1}^{3} \right)<0$，因此判决${ {\hat{u}}_{4}}=1$，此处发生译码错误。

$图 5 极化码的SC译码，对${ {u}_{4}}$译码$

总结

SC译码算法以LLR为判决准则，对每一个比特进行硬判决，按比特序号从小到大的顺序依次判决译码。当码长趋近于无穷时，由于各个分裂信道接近完全极化（其信道容量或者为0或者为1），毎个消息比特都会获得正确的译码结果，可以在理论上使得极化码达到信道的对称容量$I\left( W \right)$。而且SC译码器的复杂度仅为$O\left( N\log N \right)$和码长呈近似线性的关系。然而，在有限码长下，由于信道极化并不完全，依然会存在一些消息比特无法被正确译码。当前面$i-1$个消息比特的译码中发生错误之后，由于SC译码器在对后面的消息比特译码时需要用到之前的消息比特的估计值，这就会导致较为严重的错误传递。因此，对于有限码长的极化码，采用SC译码器往往不能达到理想的性能。

参考文献

[1] Arikan E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels[J]. IEEE Transactions on Information Theory, 2008, 55(7):3051-3073. [2] 张亮. 极化码的译码算法研究及其应用[D].浙江大学,2016.