Polar Code(4)编码之极化信道可靠性估计
前言
由Arikan发明的Polar Code经典编码算法已在《Polar
Code(2)编码原理》中阐明,《Polar
Code(3)编码实例》则是对前文的举例。在编码实例中,有两个前提假设:
- 假设一个二进制删除信道(BEC);
- 假设采用计算巴氏参数来评估各分裂子信道的可靠性。
Arikan在讨论信道极化时,针对的是二进制离散无记忆信道(B-DMC),然而在构造极化码时需要计算的巴氏参数\(Z\left( W \right)\)的适用范围是二进制删除信道。BEC是B-DMC的子集。因此在Polar Code编码时只能回落的BEC来进行构造。
当信道不是BEC信道时,比如二元对称信道(BSC)或二进制高斯白噪声信道(BAWGNC),则超出了\(Z\left( W \right)\)的适用范围,各个分裂信道的\(Z\left( W{}_{N}^{\left( i \right)} \right)\)无法精确得到。为了更精确地估计信道极化中各分裂信道的可靠性,Mori等人提出了密度进化(Density Evolution,DE)的构造方法。该方法适用于所有类型的B-DMC。
定义错误概率:对信道\(W\)的\(N\)个独立时隙上进行信道极化以后,得到极化信道\(W_{N}^{\left( i \right)}\),其中\(i=1,2,...,N\)。令事件\({ {A}_{i}}\)表示序号为\(i\)的极化信道\(W_{N}^{\left( i \right)}\)所承载的比特经过传输后接收发生错误,即
\[{ {A}_{i}}=\left\{ u_{1}^{N},y_{1}^{N}:W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}} \right)<W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}}\oplus 1 \right) \right\}\]
则极化信道\(W_{N}^{\left( i \right)}\)的错误概率为\(P\left( { {A}_{i}} \right)\)。
Marshall:关于事件\({ {A}_{i}}\)的理解详见《Answer-Polar Code-定义错误概率》。
密度进化(DE)
类似LDPC码等信道编码,信道极化也可以用Tanner图的结构来表示。下图给出了一个\(N=8\)的例子,图中圆圈表示变量节点,每个变量节点代码一个比特,同时也存储了该比特取值为0或1时的概率;而方框则表示校验节点,表示与之相连的各变量节点比特值的检验和为零。
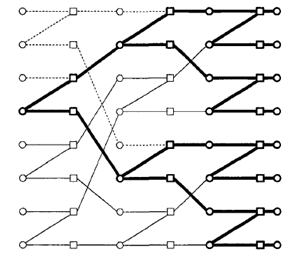
由于变量节点的比特值仅可能有0或1两种取值,因此,存储与变量节点的消息往往用对数似然比(LLR)值来表示。
\[\begin{equation} L_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1} \right)=\ln \left( \frac{W_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1}|0 \right)}{W_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1}|1 \right)} \right) \end{equation}\]
根据《Polar Code(2)编码原理》中递归式\(W_{N}^{\left( 2i-1 \right)}\left( y_{1}^{N},u_{1}^{2i-2}|{u_{2i-1}} \right)\)与式\(W_{N}^{\left( 2i \right)}\left( y_{1}^{N},u_{1}^{2i-1}|{u_{2i}} \right)\),Tanner图中各个变量节点的LLR值可以递归地计算得到
\[\begin{align} & L_{N}^{\left( 2i-1 \right)}\left( y_{1}^{N},\hat{u}_{1}^{2i-2} \right)=2{\tanh ^{-1}}\left( \tanh \left( \frac{L_{N/{2}\;}^{\left( i \right)}\left( y_{1}^{N/{2}\;},\hat{u}_{1,o}^{2i-2}\oplus \hat{u}_{1,e}^{2i-2} \right)}{2} \right) \right) \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \nonumber \cdot \tanh \left( \frac{L_{N/{2}\;}^{\left( i \right)}\left( y_{N/{2}\;+1}^{N},\hat{u}_{1,e}^{2i-2} \right)}{2} \right) \\ \end{align}\]
\[\begin{align} & L_{N}^{\left( 2i \right)}\left( y_{1}^{N},\hat{u}_{1}^{2i-1} \right)=L_{ {N}/{2}\;}^{\left( i \right)}\left( y_{ {N}/{2}\;+1}^{N},\hat{u}_{1,e}^{2i-2} \right)+{ {\left( -1 \right)}^{ { { {\hat{u}}}_{2i-1}}}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \nonumber \cdot L_{ {N}/{2}\;}^{\left( i \right)}\left( y_{1}^{ {N}/{2}\;},\hat{u}_{1,o}^{2i-2}\oplus \hat{u}_{1,e}^{2i-2} \right) \\ \end{align}\]
若最终得到的\(L_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1} \right)\ge 0\),则判决为\({\hat{u}_{i}}=0\);否则,判决\({\hat{u}_{i}}=1\)。
将某一个变量节点的LLR值视为一个随机变量,用\(\mathbf{a}\left( z \right)\)表示该随机变量的概率密度函数(PDF)。由于信道满足对称性,可以假设发送的比特为全零。从而该变量节点的比特判决值错误的概率为
\[\begin{equation} {P_{e}}=\int_{-\infty }^{0}{\mathbf{a}\left( z \right)}dz \end{equation}\]
在对第\(i\)个信道进行可靠性计算时,如上图中加粗线条所示,以比特\({u_{i}}\)对应的变量节点为根节点,逐层扩展,直至最右侧一列变量节点,构成译码树。
用\({\mathbf{a}_{w}}\)表示信道输入到最右侧一列变量节点的LLR值的PDF;用\(\mathbf{a}_{N}^{\left( i \right)}\)表示\(L_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1} \right)\)值的PDF。根据密度进化理论以及式(2)和式(3),假设发送序列为全零比特序列,在\(u_{1}^{i-1}\)值已知的条件下,序号为\(i\)的极化信道LLR值可以递归第计算如下
\[\begin{equation} \mathbf{a}_{2N}^{\left( 2i-1 \right)}=\mathbf{a}_{N}^{\left( i \right)}\odot \mathbf{a}_{N}^{\left( i \right)} \end{equation}\]
\[\begin{equation} \mathbf{a}_{2N}^{\left( 2i \right)}=\mathbf{a}_{N}^{\left( i \right)}*\mathbf{a}_{N}^{\left( i \right)} \end{equation}\]
\[\begin{equation} \mathbf{a}_{1}^{\left( 1 \right)}\text{=}{\mathbf{a}_{w}} \end{equation}\]
其中,运算$\(与\)*\(分布表示校验节点与变量节点上的卷积操作。通过概率密度函数\){N}^{( i )}\(与式(4)可以得到各个极化信道\)W{N}^{( i )}\(的可靠性度量\)P( {A_{i}} )$。
高斯近似(GA)
通过密度进化对极化信道\(W_{N}^{\left(
i \right)}\)的可靠性度量\(P\left(
{A_{i}}
\right)\)进行计算,可以适用于任意类型的B-DMC信道。然而,在实际算法实现时,需要维护一个高维的向量以存储(量化后的)概率密度函数\(\mathbf{a}_{N}^{\left( i
\right)}\)。为保证计算结果精确,该向量的维度常取到\({10^{6}}\),对如此高维的向量进行式(5)和式(6)的卷积操作,计算复杂度非常高。
在大多数研究场景下,信道编码的传输信道模型均为BAWGNC信道。在BAWGNC信道下,可以将密度进化中的LLR值的概率密度函数用一族方差为均值2倍的高斯分布来近似,从而简化成了对一维的均值的计算,大大降低计算量,这种对DE的简化计算即为高斯近似(Gaussian Approximation,GA)。
对噪声方差为\({\sigma ^{2}}\)的BAWGNC信道,调制方式采用BPSK,若从信道获取的接收信号为\(y\)。
\[\begin{equation} y=\left( 1-2x \right)+z \end{equation}\]
其中发送比特\(x\in \left\{ 0,1 \right\}\),\(z\sim N\left( 0,{\sigma ^{2}} \right)\)。
假设发送比特为全零序列,则对应的LLR值为
\[\begin{equation} LLR\left( y \right)=\ln \frac{p\left( y|x=0 \right)}{p\left( y|x=1 \right)}=\frac{2}{\sigma ^{2}}y \end{equation}\]
其中\(y\sim N\left( 1,{\sigma ^{2}} \right)\)。因此式(9)中所得的LLR值符合均值为\(2/{\sigma ^{2}}\;\)、方差为\(4/{\sigma ^{2}}\;\)的高斯分布。根据已有的高斯近似理论,若输入的消息\(\mathbf{a}_{N/{2}\;}^{\left( i \right)}\)服从独立的高斯分布,对如式(6)所示的变量节点上的操作,则其输出\(\mathbf{a}_{N}^{\left( i \right)}\)也服从高斯分布;对如式(5)所示的变量节点上的操作,其输出\(\mathbf{a}_{N}^{\left( 2i-1 \right)}\)也非常接近高斯分布。由于高斯分布可以有其均值和方差完全决定,因此在概率密度函数的计算过程中值需要考虑均值和方差,但必需满足密度进化的对称条件。如果用\(f\left( z \right)\)表示LLR的概率密度,则对称条件表示为\(f\left( z \right)\text{=}f\left( -z \right){e^{z}}\)。对于均值为\(m\)、方差为\({\sigma ^{2}}\)的高斯分布,该对称条件可以简化为\({\sigma ^{2}}=2m\)。因此,在高斯近似中,仅需要考虑一维的变量,即均值\(m\)。设\(\mathbf{a}_{N}^{\left( i \right)}\)可以用\(N\left( m_{N}^{\left( i \right)},2m_{N}^{\left( i \right)} \right)\)表示,则式(5)、式(6)和式(7)中所示的LLR计算过程可以用高斯近似成为
\[\begin{equation} m_{2N}^{\left( 2i \right)}={ {\varphi }^{-1}}\left( 1-{ {\left[ 1-\varphi \left( m_{N}^{\left( i \right)} \right) \right]}^{2}} \right) \end{equation}\]
\[\begin{equation} m_{2N}^{\left( 2i \right)}=2m_{N}^{\left( i \right)} \end{equation}\]
\[\begin{equation} m_{1}^{\left( 1 \right)}={2}/{ { {\sigma }^{2}}}\; \end{equation}\]
其中函数
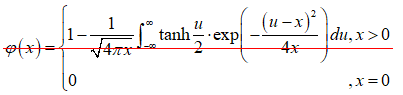
\[\begin{equation} \varphi \left( x \right)=\left\{ \begin{matrix} 1-\frac{1}{\sqrt{4\pi x}}\int_{-\infty }^{\infty }{\tanh \frac{u}{2}\cdot \exp \left( -\frac{ { {\left( u-x \right)}^{2}}}{4x} \right)du,x>0} \\ 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0 \\ \end{matrix} \right. \end{equation}\]
注:文献[2]中的公式有误。
\(\varphi \left( x \right)\)在\(\left[ 0,\infty \right)\)上连续单调递减,\(\varphi \left( 0 \right)\text{=}1\),\(\varphi \left( \infty \right)\text{=0}\),其反函数用\({ {\varphi }^{-1}}\left( x \right)\)表示。一般情况下,函数\(\varphi \left( x \right)\)可以使用如下的近似形式计算
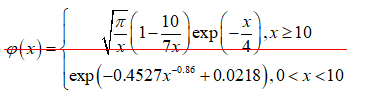
\[\begin{equation} \varphi \left( x \right)=\left\{ \begin{matrix} \sqrt{\frac{\pi }{x}}\left( 1-\frac{10}{7x} \right)\exp \left( -\frac{x}{4} \right),x\ge 10 \\ \exp \left( -0.4527{ {x}^{0.86}}+0.0218 \right),0<x<10 \\ \end{matrix} \right. \end{equation}\]
注:文献[2]中的公式有误。
在得到\(m_{N}^{\left( i \right)}\)后,各极化信道\(W_{N}^{\left( i \right)}\)在发送全零时对应的接收信号LLR值服从分布\(N\left( m_{N}^{\left( i \right)},2m_{N}^{\left( i \right)} \right)\),于是可靠性度量\(P\left( { {A}_{i}} \right)\)即可计算如下
\[\begin{equation} P\left( { {A}_{i}} \right)\text{=}\int\limits_{-\infty }^{0}{\frac{1}{2\sqrt{\pi m_{N}^{\left( i \right)}}}\cdot \exp \left( \frac{-{ {\left( x-m_{N}^{\left( i \right)} \right)}^{2}}}{4m_{N}^{\left( i \right)}} \right)}dx \end{equation}\]
总结
巴氏参数、密度进化和高斯近似法都是计算各分裂信道错误概率\(P\left( { {A}_{i}}
\right)\)的方法,不同的方法有各自的适用范围。巴氏参数法仅适用于BEC,密度进化法适用于所有类型的B-DMC,而高斯近似法则适用于更加实际的BAWGNC。
参考文献
[1] Arikan E. Channel Polarization: A Method for Constructing
Capacity-Achieving Codes for Symmetric Binary-Input Memoryless
Channels[J]. IEEE Transactions on Information Theory, 2008,
55(7):3051-3073. [2] 陈凯. 极化编码理论与实用方案研究[D]. 北京邮电大学,
2014.