Polar Code(7)SCL译码算法
前言
Polar Code在码长趋于无穷时,信道极化才越完全。但在有限码长下,由于信道极化并不完全,依然会存在一些信息比特无法被正确译码。当前面\(i-1\)个信息比特的译码中发生错误之后,由于SC译码器在对后面的信息比特译码时需要用到之前的信息比特的估计值,这就会导致较为严重的错误传递。SC译码算法是一种贪婪算法,对码树的每一层仅仅搜索到最优路径就进行下一层,所以无法对错误进行修改。SCL译码算法就是对SC算法的改进。但在SCL之前,先来看看SC译码算法的码树表示。
SC译码算法的码树表示
根据极化码在SC译码下各个比特判决之间的依赖关系,能够构造一颗码树 \(\Gamma = \left( \varepsilon, V \right)\),其中 \(\varepsilon\) 和 \(V\) 分别表示码树中的边和节点集合。定义节点的深度为该节点到根节点的最短路径长度,对于一个码长为 \(N\) 的极化码,其码树节点集合\(V\) 能够按照深度 \(d\) 划分成 \(N+1\) 个子集,记作 \(V_d\),其中 \(d = 0,1,...,N\)。特别地,\(V_0\) 仅包含根节点,即 \(\left| V_0 \right| = 1\)。除了叶节点(即 \(d = N\) 时),码树 \(\Gamma\) 中的每一个节点 \(v \in V_d\) 均分别通过两条标记着 0、1 的边与两个 \(V_{d+1}\) 中的后继节点相连。某一个节点 \(v\) 所对应的序列 \(u_1^d\) 的值定义为从根节点开始到达该节点 \(v\) 所需经过的各个边的标记序列。例如,若某一个节点 \(v\) 表示了序列 \(u_1^i\),则其左、右后继节点分别代表了路径 \(\left( u_1^i, u_1^{i+1} = 0 \right)\) 与 \(\left( u_1^i, u_1^{i+1} = 1 \right)\)。于是,从根节点到每一个深度为 \(d\) 的节点 \(v\in V_d\) 的路径,均对应了一种 \(u_1^d\) 可能的取值,由于信源序列为二进制比特序列,所以 \(\left| V_d \right| = 2^d\)。定义连接着深度为 \(i-1\) 和 \(i\) 的节点的边所构成的集合为第 \(i\) 层边,记作 \(\varepsilon_i\)。显然,对任意 \(i \in \left\{1,2,...,N \right\}\),有 \(\left| \varepsilon_i \right| = 2^i\)。从根节点到任何一个节点所形成的路径,均对应一个路径度量值(PM)。值得注意的是,该码树结构仅与码长 \(N\) 有关。极化码译码码树实质上是一个满二叉树,因此译码过程也就是在满二叉树上寻找合适的路径。如图 1 所示,给出了一个当 \(N = 4\) 时极化码码树的示例,各节点旁的数字指示了对应的转移概率,在每个节点处选择转移概率最大的路径,最终译码序列为 \(\hat{u}_1^N = \left[ \begin{matrix} 0 & 0 & 1 & 1 \end{matrix} \right]\)。

SCL译码算法
针对SC译码算法的缺点,一个直接的改进方案是,增加每一层路径搜索后允许保留的候选路径数量,从仅允许选择“最好的一条路径进行下一步扩展”改为“最大允许选择最好的 条路径进行下一步扩展”,其中\(L\ge 1\)。与SC算法一样,改进的算法依然从码树根节点开始,逐层依次向叶子节点层进行路径搜索。不同的是,每一层扩展后,尽可能多地保留后继路径(每一层保留的路径数不大于\(L\))。完成一层的路径扩展后,选择路径度量值(Path Metrics,PM)最小的\(L\)条,保存在一个列表中,等待进行下一层的扩展。因此称该算法为串行抵消列表(Successive Cancellation List,SCL)译码算法,并称参数\(L\)为搜索宽度。当\(L=1\)时,SCL译码算法退化为SC译码算法;当\(L\ge { {2}^{K}}\)时,SCL译码等价于最大似然译码。
思考
现在思考一个问题:如图2所示,当Polar Code编译码结构用“蝶形图”表示时,在译码时只需要在每个节点处计算相应的对数似然比,从右到左依次计算,并最终得到\(L_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1} \right)\),若LLR值为非负则判决\({ {\hat{u}}_{i}}=0\),否则判决\({ {\hat{u}}_{i}}=1\)。一共有\(N\log N\)个节点,因此相应地也要计算\(N\log N\)个LLR。对于图2来说这一过程没有任何问题。
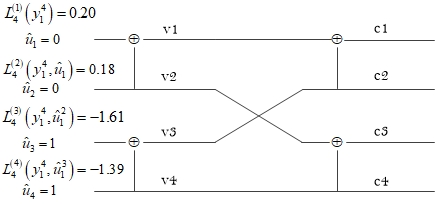
现在转换思路,将译码结构用二叉树表示,一个LLR值指示了每个节点两条支路上的转移概率的比值关系。如果像图1那样,每条支路就用转移概率来表征,向左是发送为比特0的转移概率,向右是发送为比特1的转移概率。当然这样也可以,对于SC译码来说,图1使用转移概率和图2使用对数似然比实际上是等价的。但随着码长的增加,转移概率函数的数值会越来越小,译码器存在着下溢的风险,所以通常不直接使用转移概率。由于SC译码过程实质上是二值判决,因此通常还是要采用转移概率的对数似然比。
现在可以明确两点:一是使用对数似然比,二是在满二叉树上使用对数似然比。但仍然存在的问题是:SC算法实际上是SCL算法的特例,即搜索宽度\(L=1\)的情况;对于\(L\ge 2\)的情况,单单依靠LLR是无法在\(2L\)个后继节点中挑选\(L\)个最优节点作为后继译码路径的。这就需要在LLR的基础上对\(2L\)条路径度量值进行计算,以便可以实现在对数似然域上的SCL译码算法。因此需要明确的第三点就是:重新定义路径度量值(PM)。
路径度量值
在SCL译码过程中,存在\(L\)条路径同时进行译码搜索,对于任意一条路径\(l\in \left\{ 1,2,...,L \right\}\)以及任意发送比特\({ {u}_{i}}\)(\(i\in \left\{ 1,2,...,N \right\}\)),其对应的路径度量值定义如下:
\[\begin{align} PM_{l}^{\left( i \right)}\triangleq \sum\limits_{j=1}^{i}{\ln \left( 1+\exp \left( -\left( 1-2{ { {\hat{u}}}_{j}}\left[ l \right] \right)\cdot L_{N}^{\left( j \right)} \right) \right)} \end{align}\]
其中,\(L_{N}^{\left( j \right)}\left[ l \right]=\ln \frac{W_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1}\left[ l \right]|0 \right)}{W_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1}\left[ l \right]|1 \right)}\)。
如果发送端所有信息比特在\(\left\{ 0,1 \right\}\)上均匀分布,那么对于任意两条不同路径\({ {l}_{1}},{ {l}_{2}}\in \left\{ 1,2,...,L \right\}\),当且仅当\(PM_{ { {l}_{1}}}^{\left( i \right)}>PM_{ { {l}_{2}}}^{\left( i \right)}\)成立时,有如下关系成立:
\[\begin{align} W_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1}\left[ { {l}_{1}} \right]|\hat{u}_{1}^{i}\left[ { {l}_{1}} \right] \right)<W_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1}\left[ { {l}_{2}} \right]|\hat{u}_{1}^{i}\left[ { {l}_{2}} \right] \right) \end{align}\]
由上式可见,路径对应的转移概率越大,路径度量值越小。基于这种关系就完全可以在对数似然比上对\(2L\)条路径进行挑选。式(1)可以近似表示为
\[\begin{align} \nonumber PM_{l}^{\left( i \right)}\approx \left\{ \begin{matrix} PM_{l}^{\left( i-1 \right)},\ \ if\ { { {\hat{u}}}_{i}}\left[ l \right]=\delta \left( L_{N}^{\left( i \right)}\left[ l \right] \right) \\ PM_{l}^{\left( i-1 \right)}+\left| L_{N}^{\left( i \right)}\left[ l \right] \right|,\ \ if\ { { {\hat{u}}}_{i}}\left[ l \right]\ne \delta \left( L_{N}^{\left( i \right)}\left[ l \right] \right) \\ \end{matrix} \right. \end{align}\]
但考虑译码过程中包含了信息比特和冻结比特,因此上式可以改写为
\[PM_{l}^{\left( i \right)}=\left\{ \begin{align} \nonumber & PM_{l}^{\left( i-1 \right)}\ \ ,\ if\ { {u}_{i}}\ is\ \text{information or frozen bit}\ and\text{ }{ { {\hat{u}}}_{i}}\left[ l \right]=\delta \left( L_{N}^{\left( i \right)}\left[ l \right] \right) \\ & PM_{l}^{\left( i-1 \right)}+\left| L_{N}^{\left( i \right)}\left[ l \right] \right|,\ if\ { {u}_{i}}\ is\ \text{information or frozen bit}\ and\text{ }{ { {\hat{u}}}_{i}}\left[ l \right]\ne \delta \left( L_{N}^{\left( i \right)}\left[ l \right] \right) \\ \nonumber & +\infty \ \ ,\ if\ { {u}_{i}}\ is\ \text{frozen bit}\ and\ \text{incorrect value} \\ \end{align} \right.\]
其中\(\delta \left( x \right)=\frac{1}{2}\left( 1-sign\left( x \right) \right)\),\(PM_{l}^{\left( 0 \right)}=0\)。对于信息比特的判决有
\[\begin{align} { {\hat{u}}_{i}}=\delta \left( L_{N}^{\left( i \right)}\left( y_{1}^{N},\hat{u}_{1}^{i-1} \right) \right) \end{align}\]
SCL译码示例
下面仍然以《Polar Code(6)SC译码算法》中的SC译码的例子为例来说明SCL算法的具体实现过程。给定发送端原始比特序列\(u_{1}^{4}=\left( \begin{matrix} { {u}_{1}} & { {u}_{2}} & { {u}_{3}} & { {u}_{4}} \\ \end{matrix} \right)=\left( \begin{matrix} 0 & 0 & 0 & 0 \\ \end{matrix} \right)\),其中\({ {u}_{1}}\)为冻结比特,\(u_{2}^{4}\)为信息比特。经过Polar编码以后通过AWGN信道传输。假设接收端已知各子信道对数似然比\(L_{1}^{\left( 1 \right)}\left( y_{1}^{4} \right)=\left[ \begin{matrix} 1.5 & 2 & -1 & 0.5 \\ \end{matrix} \right]\)。
每一条路径都拥有自己的一套LLR值,每一条路径的PM都要根据各自路径上的LLR值计算。以a、b、c、d表示路径1、路径2、路径3、路径4。为了便于说明SCL译码过程,PM值直接标注在示意图上,LLR值则用一个向量来表示。
搜索第一层
计算第1个比特相关的LLR
\[L_{4}^{\left( 1 \right)}\left( y_{1}^{4} \right)=f\left( L_{2}^{\left( 1 \right)}\left( y_{1}^{2} \right),L_{2}^{\left( 1 \right)}\left( y_{3}^{4} \right) \right)\]
其中,\(L_{2}^{\left( 1 \right)}\left( y_{1}^{2} \right)\)和\(L_{2}^{\left( 1 \right)}\left( y_{3}^{4} \right)\)递归地计算为
\[L_{2}^{\left( 1 \right)}\left( y_{1}^{2} \right)=f\left( L_{1}^{\left( 1 \right)}\left( { {y}_{1}} \right),L_{1}^{\left( 1 \right)}\left( { {y}_{2}} \right) \right)=f\left( 1.5,2 \right)=1.06\]
\[L_{2}^{\left( 1 \right)}\left( y_{3}^{4} \right)=f\left( L_{1}^{\left( 1 \right)}\left( { {y}_{3}} \right),L_{1}^{\left( 1 \right)}\left( { {y}_{4}} \right) \right)=f\left( -1,0.5 \right)=-0.23\]
从而,\[L_{4}^{\left( 1 \right)}\left( y_{1}^{4} \right)=f\left( 1.06,-0.23 \right)=-0.11\]。
建立向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} -0.11 & -0.11 \\ \end{matrix} \right]\]
计算候选路径的度量值
a. 0
\(L_{4}^{\left( 1 \right)}\)取向量\(\mathbf{LLR}\)的 第1元素 ,即\(L_{4}^{\left( 1 \right)}=-0.11\);比特估计值\({ {\hat{u}}_{1}}=0\)。
\(\delta \left( L_{4}^{\left( 1 \right)} \right)=\frac{1}{2}\left( 1-sign\left( -0.11 \right) \right)=1\)。由于\({ {u}_{1}}\)是冻结比特,但\({ {\hat{u}}_{1}}\ne \delta \left( L_{4}^{\left( 1 \right)} \right)\),所以有
\[PM\left( { { {\hat{u}}}_{1}}=0 \right)=PM_{1}^{\left( 0 \right)}+\left| L_{4}^{\left( 1 \right)} \right|=0+0.11=0.11\]
b. 1
\(L_{4}^{\left( 1 \right)}\)取向量\(\mathbf{LLR}\)的 第2元素 ,即\(L_{4}^{\left( 1 \right)}=-0.11\);比特估计值\({ {\hat{u}}_{1}}=1\)。
\(\delta \left( L_{4}^{\left( 1 \right)} \right)=\frac{1}{2}\left( 1-sign\left( -0.11 \right) \right)=1\)。由于\({ {u}_{1}}\)是冻结比特,但此时\({ {\hat{u}}_{1}}=1\)显然取值错误,所以有
\[PM\left( { { {\hat{u}}}_{1}}=1 \right)=\text{+}\infty \]
路径扩展
如图3所示,由于搜索宽度已达到\(L=2\),因此第1层的2条路径均保留。继续在下一层扩展,至\(2L\)条路径,再从中挑选\(L\)条。
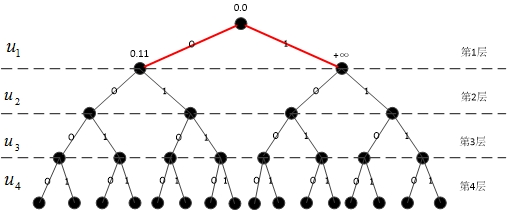
搜索第二层
计算第2个比特相关的LLR
分别计算\(2L\)条路径在第2层对应的LLR。
a. 00
比特估计值\({ {\hat{u}}_{1}}=0\),所以有
\[\nonumber \begin{align} & L_{4}^{\left( 2 \right)}\left( y_{1}^{4},{ { {\hat{u}}}_{1}} \right)=g\left( L_{2}^{\left( 1 \right)}\left( y_{1}^{2} \right),L_{2}^{\left( 1 \right)}\left( y_{3}^{4} \right),{ { {\hat{u}}}_{1}} \right)\text{=}g\left( 1.06,-0.23,0 \right) \\ \nonumber & ={ {\left( -1 \right)}^{0}}\times 1.06+\left( -0.23 \right) \\ \nonumber & =0.83 \\ \end{align}\]
重新建立向量LLR
\[\mathbf{LLR}=\left[ 0.83 \right]\]
b. 01
同上,\(L_{4}^{\left( 2 \right)}\left( y_{1}^{4},{ { {\hat{u}}}_{1}} \right)=0.83\)。
更新向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} 0.83 & 0.83 \\ \end{matrix} \right]\]
c. 10
比特估计值\({ {\hat{u}}_{1}}=1\),所以有
\[\begin{align} \nonumber & L_{4}^{\left( 2 \right)}\left( y_{1}^{4},{ { {\hat{u}}}_{1}} \right)=g\left( L_{2}^{\left( 1 \right)}\left( y_{1}^{2} \right),L_{2}^{\left( 1 \right)}\left( y_{3}^{4} \right),{ { {\hat{u}}}_{1}} \right)\text{=}g\left( 1.06,-0.23,1 \right) \\ \nonumber & ={ {\left( -1 \right)}^{1}}\times 1.06+\left( -0.23 \right) \\ \nonumber & =-1.29 \\ \end{align}\\]
更新向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} \begin{matrix} 0.83 & 0.83 \\ \end{matrix} & -1.29 \\ \end{matrix} \right]\]
d. 11
同上,\(L_{4}^{\left( 2 \right)}\left( y_{1}^{4},{ { {\hat{u}}}_{1}} \right)=-1.29\)。
更新向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} \begin{matrix} \begin{matrix} 0.83 & 0.83 \\ \end{matrix} & -1.29 \\ \end{matrix} & -1.29 \\ \end{matrix} \right]\]
计算候选路径的度量值
由于在上一层已经扩展至\(L\)条路径,那么在这一层将会计算\(2L\)条路径的度量值,然后保留PM最小的\(L\)条路径,并且删除其余路径。
a. 00
\(L_{4}^{\left( 2 \right)}\)取向量\(\mathbf{LLR}\)的 第1元素 ,即\(L_{4}^{\left( 2 \right)}=0.83\);比特估计值\({ {\hat{u}}_{2}}=0\)。
\(\delta \left( L_{4}^{\left( 2 \right)} \right)=\frac{1}{2}\left( 1-sign\left( 0.83 \right) \right)=0\)。由于\({ {u}_{2}}\)为信息比特,且\({ {\hat{u}}_{2}}=\delta \left( L_{4}^{\left( 2 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{2}=00 \right)=PM\left( { { {\hat{u}}}_{1}}=0 \right)=0.11\]
b. 01
\(L_{4}^{\left( 2 \right)}\)取向量\(\mathbf{LLR}\)的 第2元素 ,即\(L_{4}^{\left( 2 \right)}=0.83\);比特估计值\({ {\hat{u}}_{2}}=1\)。
\(\delta \left( L_{4}^{\left( 2 \right)} \right)=\frac{1}{2}\left( 1-sign\left( 0.83 \right) \right)=0\)。由于\({ {u}_{2}}\)为信息比特,且\({ {\hat{u}}_{2}}\ne \delta \left( L_{4}^{\left( 2 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{2}=01 \right)=PM\left( { { {\hat{u}}}_{1}}=0 \right)+\left| L_{4}^{\left( 2 \right)} \right|\text{=0}\text{.11+}0.83=0.94\]
截止目前的扩展路径如图4所示。
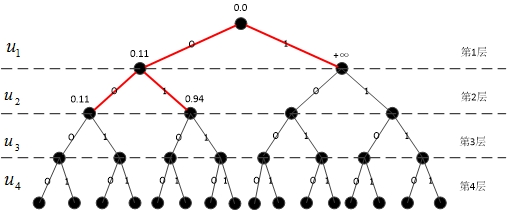
c. 10
\(L_{4}^{\left( 2 \right)}\)取向量\(\mathbf{LLR}\)的 第3元素 ,即\(L_{4}^{\left( 2 \right)}=-1.29\);比特估计值\({ {\hat{u}}_{2}}=0\)。
\(\delta \left( L_{4}^{\left( 2 \right)} \right)=\frac{1}{2}\left( 1-sign\left( -1.29 \right) \right)=1\)。由于\({ {u}_{2}}\)为信息比特,且\({ {\hat{u}}_{2}}\ne \delta \left( L_{4}^{\left( 2 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{2}=10 \right)=PM\left( { { {\hat{u}}}_{1}}=1 \right)\text{+}L_{4}^{\left( 2 \right)}\text{=}+\infty +1.29\to +\infty \]
d. 11
\(L_{4}^{\left( 2 \right)}\)取向量\(\mathbf{LLR}\)的 第4元素 ,即\(L_{4}^{\left( 2 \right)}=-1.29\);比特估计值\({ {\hat{u}}_{2}}=1\)。
\(\delta \left( L_{4}^{\left( 2 \right)} \right)=\frac{1}{2}\left( 1-sign\left( -1.29 \right) \right)=1\)。由于\({ {u}_{2}}\)为信息比特,且\({ {\hat{u}}_{2}}=\delta \left( L_{4}^{\left( 2 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{2}=11 \right)=PM\left( { { {\hat{u}}}_{1}}=1 \right)\text{=}+\infty \]
截止目前的扩展路径如图5所示。

剪枝
将已经计算出的\(2L\)路径按照PM值从小到大排序,对这\(2L\)条路径进行剪枝操作:保留\(L\)条PM值最小的路径,并且删掉其余路径。如图6所示,被保留的路径为红色,被剪枝的路径均已变成灰色。
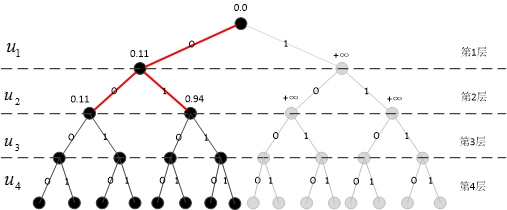
搜索第三层
分别计算 条路径在第3层对应的LLR。
计算第3个比特相关的LLR
a. 000
比特估计值\(\hat{u}{}_{1}=0,\hat{u}{}_{2}=0\)。
\[L_{4}^{\left( 3 \right)}\left( y_{1}^{4},\hat{u}_{1}^{2} \right)=f\left( L_{2}^{\left( 2 \right)}\left( y_{1}^{2},\hat{u}{}_{1}\oplus { { {\hat{u}}}_{2}} \right),L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ { {\hat{u}}}_{2}} \right) \right)\]
其中,\(L_{2}^{\left( 2 \right)}\left( y_{1}^{2},\hat{u}{}_{1}\oplus { { {\hat{u}}}_{2}} \right)\)和\(L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ { {\hat{u}}}_{2}} \right)\)递归地计算为
\[\begin{align} \nonumber & L_{2}^{\left( 2 \right)}\left( y_{1}^{2},\hat{u}{}_{1}\oplus { { {\hat{u}}}_{2}} \right)=g\left( L_{1}^{\left( 1 \right)}\left( { {y}_{1}} \right),L_{1}^{\left( 1 \right)}\left( { {y}_{2}} \right),\hat{u}{}_{1}\oplus { { {\hat{u}}}_{2}} \right)=g\left( 1.5,2,0 \right) \\ \nonumber & ={ {\left( -1 \right)}^{0}}\times 1.5+2 \\ \nonumber & =3.5 \\ \end{align}\]
\[\begin{align} \nonumber & L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ { {\hat{u}}}_{2}} \right)=g\left( L_{1}^{\left( 1 \right)}\left( { {y}_{3}} \right),L_{1}^{\left( 1 \right)}\left( { {y}_{4}} \right),{ { {\hat{u}}}_{2}} \right)=g\left( -1,0.5,0 \right) \\ \nonumber & ={ {\left( -1 \right)}^{0}}\times \left( -1 \right)+0.5 \\ \nonumber & =-0.5 \\ \end{align}\]
从而,\(L_{4}^{\left( 3 \right)}\left( y_{1}^{4},\hat{u}_{1}^{2} \right)=f\left( 3.5,-0.5 \right)=-0.47\)。
重新建立向量LLR
\[\mathbf{LLR}=\left[ -0.47 \right]\]
b. 001
同上,\(L_{4}^{\left( 3 \right)}\left( y_{1}^{4},\hat{u}_{1}^{2} \right)=f\left( 3.5,-0.5 \right)=-0.47\)。
更新向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} -0.47 & -0.47 \\ \end{matrix} \right]\]
c. 010
比特估计值\(\hat{u}{}_{1}=0,\hat{u}{}_{2}=1\)。
\[\begin{align} \nonumber & L_{2}^{\left( 2 \right)}\left( y_{1}^{2},\hat{u}{}_{1}\oplus { { {\hat{u}}}_{2}} \right)=g\left( L_{1}^{\left( 1 \right)}\left( { {y}_{1}} \right),L_{1}^{\left( 1 \right)}\left( { {y}_{2}} \right),\hat{u}{}_{1}\oplus { { {\hat{u}}}_{2}} \right)=g\left( 1.5,2,1 \right) \\ \nonumber & ={ {\left( -1 \right)}^{1}}\times 1.5+2 \\ \nonumber & =0.5 \\ \end{align}\]
\[\begin{align} \nonumber & L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ { {\hat{u}}}_{2}} \right)=g\left( L_{1}^{\left( 1 \right)}\left( { {y}_{3}} \right),L_{1}^{\left( 1 \right)}\left( { {y}_{4}} \right),{ { {\hat{u}}}_{2}} \right)=g\left( -1,0.5,1 \right) \\ \nonumber & ={ {\left( -1 \right)}^{1}}\times \left( -1 \right)+0.5 \\ \nonumber & =1.5 \\ \end{align}\]
从而,\(L_{4}^{\left( 3 \right)}\left( y_{1}^{4},\hat{u}_{1}^{2} \right)=f\left( 0.5,1.5 \right)=0.31\)。
更新向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} \begin{matrix} -0.47 & -0.47 \\ \end{matrix} & 0.31 \\ \end{matrix} \right]\]
d. 011
同上,\(L_{4}^{\left( 3 \right)}\left( y_{1}^{4},\hat{u}_{1}^{2} \right)=f\left( 0.5,1.5 \right)=0.31\)。
更新向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} \begin{matrix} \begin{matrix} -0.47 & -0.47 \\ \end{matrix} & 0.31 \\ \end{matrix} & 0.31 \\ \end{matrix} \right]\]
计算候选路径的度量值
分别计算\(2L\)条路径的度量值。
a. 000
\(L_{4}^{\left( 3 \right)}\)取向量\(\mathbf{LLR}\)的 第1元素 ,即\(L_{4}^{\left( 3 \right)}=-0.47\);比特估计值\({ {\hat{u}}_{3}}=0\)。
\(\delta \left( L_{4}^{\left( 3 \right)} \right)=\frac{1}{2}\left( 1-sign\left( -0.47 \right) \right)=1\)。由于\({ {u}_{3}}\)为信息比特,且\({ {\hat{u}}_{3}}\ne \delta \left( L_{4}^{\left( 3 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{3}=000 \right)=PM\left( \hat{u}_{1}^{2}=00 \right)+\left| L_{4}^{\left( 3 \right)} \right|=0.11+0.47=0.58\]
b. 001
\(L_{4}^{\left( 3 \right)}\)取向量\(\mathbf{LLR}\)的 第2元素 ,即\(L_{4}^{\left( 3 \right)}=-0.47\);比特估计值\({ {\hat{u}}_{3}}=1\)。
\(\delta \left( L_{4}^{\left( 3 \right)} \right)=\frac{1}{2}\left( 1-sign\left( -0.47 \right) \right)=1\)。由于\({ {u}_{3}}\)为信息比特,且\({ {\hat{u}}_{3}}=\delta \left( L_{4}^{\left( 3 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{3}=001 \right)=PM\left( \hat{u}_{1}^{2}=00 \right)\text{=}0.11\]
截止目前的扩展路径如图7所示。
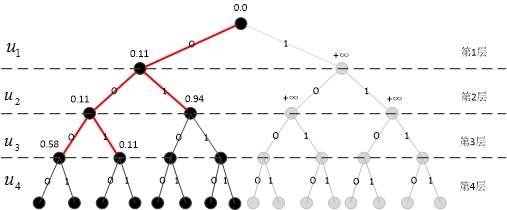
c. 010
\(L_{4}^{\left( 3 \right)}\)取向量\(\mathbf{LLR}\)的 第3元素 ,即\(L_{4}^{\left( 3 \right)}=0.31\);比特估计值\({ {\hat{u}}_{3}}=0\)。
\(\delta \left( L_{4}^{\left( 3 \right)} \right)=\frac{1}{2}\left( 1-sign\left( 0.31 \right) \right)=0\)。由于\({ {u}_{3}}\)为信息比特,且\({ {\hat{u}}_{3}}=\delta \left( L_{4}^{\left( 3 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{3}=010 \right)=PM\left( \hat{u}_{1}^{2}=01 \right)=0.94\]
d. 011
\(L_{4}^{\left( 3 \right)}\)取向量\(\mathbf{LLR}\)的 第4元素 ,即\(L_{4}^{\left( 3 \right)}=0.31\);比特估计值\({ {\hat{u}}_{3}}=1\)。
\(\delta \left( L_{4}^{\left( 3 \right)} \right)=\frac{1}{2}\left( 1-sign\left( 0.31 \right) \right)=0\)。由于\({ {u}_{3}}\)为信息比特,且\({ {\hat{u}}_{3}}\ne \delta \left( L_{4}^{\left( 3 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{3}=011 \right)=PM\left( \hat{u}_{1}^{2}=01 \right)+L_{4}^{\left( 3 \right)}=0.94+0.31=1.25\]
截止目前的扩展路径如图8所示。
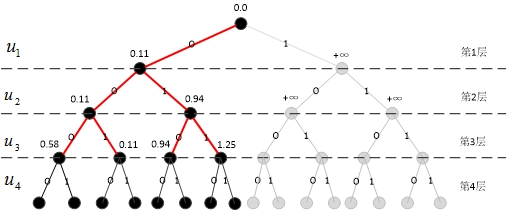
剪枝
将已经计算出的\(2L\)路径按照PM值从小到大排序,对这\(2L\)条路径进行剪枝操作:保留\(L\)条PM值最小的路径,并且删掉其余路径。如图9所示,被保留的路径为红色,被剪枝的路径均已变成灰色。
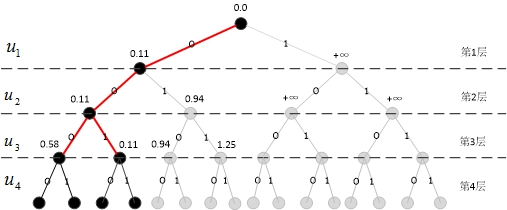
搜索第四层
计算第4个比特相关的LLR
分别计算\(2L\)条路径在第4层对应的LLR。
a. 0000
比特估计值\(\hat{u}{}_{1}=0,\hat{u}{}_{2}=0,\hat{u}{}_{3}=0\)。
\[\begin{align} \nonumber & L_{4}^{\left( 4 \right)}\left( y_{1}^{4},\hat{u}_{1}^{3} \right)=g\left( L_{2}^{\left( 2 \right)}\left( y_{1}^{2},{ { {\hat{u}}}_{1}}\oplus { { {\hat{u}}}_{2}} \right),L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ { {\hat{u}}}_{2}} \right),{ { {\hat{u}}}_{3}} \right)=g\left( 3.5,-0.5,0 \right) \\ \nonumber & ={ {\left( -1 \right)}^{0}}\times 3.5+\left( -0.5 \right) \\ \nonumber & =3 \\ \end{align}\]
重新建立向量LLR
\[\mathbf{LLR}=\left[ 3 \right]\]
b. 0001
同上,\(L_{4}^{\left( 4 \right)}\left( y_{1}^{4},\hat{u}_{1}^{3} \right)=3\)。
更新向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} 3 & 3 \\ \end{matrix} \right]\]
c. 0010
比特估计值\(\hat{u}{}_{1}=0,\hat{u}{}_{2}=0,\hat{u}{}_{3}=1\)。
\[\begin{align} \nonumber & L_{4}^{\left( 4 \right)}\left( y_{1}^{4},u_{1}^{3} \right)=g\left( L_{2}^{\left( 2 \right)}\left( y_{1}^{2},{ {u}_{1}}\oplus { {u}_{2}} \right),L_{2}^{\left( 2 \right)}\left( y_{3}^{4},{ {u}_{2}} \right),{ {u}_{3}} \right)=g\left( 3.5,-0.5,1 \right) \\ \nonumber & ={ {\left( -1 \right)}^{1}}\times 3.5+\left( -0.5 \right) \\ \nonumber & =-4 \\ \end{align}\]
更新向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} 3 & 3 & -4 \\ \end{matrix} \right]\]
d. 0011
同上,\(L_{4}^{\left( 4 \right)}\left( y_{1}^{4},\hat{u}_{1}^{3} \right)=-4\)。
更新向量LLR
\[\mathbf{LLR}=\left[ \begin{matrix} \begin{matrix} 3 & 3 & -4 \\ \end{matrix} & -4 \\ \end{matrix} \right]\]
计算候选路径的度量值
终于到最后一层了,继续计算\(2L\)个路径的度量值。
a. 0000
\(L_{4}^{\left( 4 \right)}\)取向量\(\mathbf{LLR}\)的 第1元素 ,即\(L_{4}^{\left( 4 \right)}=3\);比特估计值\({ {\hat{u}}_{4}}=0\)。
\(\delta \left( L_{4}^{\left( 4 \right)} \right)=\frac{1}{2}\left( 1-sign\left( 3 \right) \right)=0\)。由于\({ {u}_{4}}\)为信息比特,且\({ {\hat{u}}_{4}}=\delta \left( L_{4}^{\left( 4 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{4}=0000 \right)=PM\left( \hat{u}_{1}^{3}=000 \right)=0.58\]
b. 0001
\(L_{4}^{\left( 4 \right)}\)取向量\(\mathbf{LLR}\)的 第2元素 ,即\(L_{4}^{\left( 4 \right)}=3\);比特估计值\({ {\hat{u}}_{4}}=1\)。
\(\delta \left( L_{4}^{\left( 4 \right)} \right)=\frac{1}{2}\left( 1-sign\left( 3 \right) \right)=0\)。由于\({ {u}_{4}}\)为信息比特,且\({ {\hat{u}}_{4}}\ne \delta \left( L_{4}^{\left( 4 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{4}=0001 \right)=PM\left( \hat{u}_{1}^{3}=000 \right)+L_{4}^{\left( 4 \right)}=0.58+3=3.58\]
截止目前的扩展路径如图10所示。
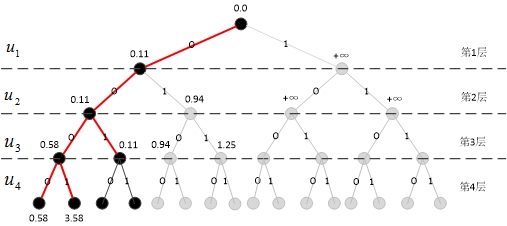
c. 0010
\(L_{4}^{\left( 4 \right)}\)取向量\(\mathbf{LLR}\)的 第3元素 ,即\(L_{4}^{\left( 4 \right)}=-4\);比特估计值\({ {\hat{u}}_{4}}=0\)。
\(\delta \left( L_{4}^{\left( 4 \right)} \right)=\frac{1}{2}\left( 1-sign\left( -4 \right) \right)=1\)。由于\({ {u}_{4}}\)为信息比特,且\({ {\hat{u}}_{4}}\ne \delta \left( L_{4}^{\left( 4 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{4}=0010 \right)=PM\left( \hat{u}_{1}^{3}=001 \right)+\left| L_{4}^{\left( 4 \right)} \right|=0.11+4=4.\text{11}\]
d. 0011
\(L_{4}^{\left( 4 \right)}\)取向量\(\mathbf{LLR}\)的 第4元素 ,即\(L_{4}^{\left( 4 \right)}=-4\);比特估计值\({ {\hat{u}}_{4}}=1\)。
\(\delta \left( L_{4}^{\left( 4 \right)} \right)=\frac{1}{2}\left( 1-sign\left( -4 \right) \right)=1\)。由于\({ {u}_{4}}\)为信息比特,且\({ {\hat{u}}_{4}}=\delta \left( L_{4}^{\left( 4 \right)} \right)\),所以有
\[PM\left( \hat{u}_{1}^{4}=0011 \right)=PM\left( \hat{u}_{1}^{3}=001 \right)=0.11\]
截止目前的扩展路径如图11所示。
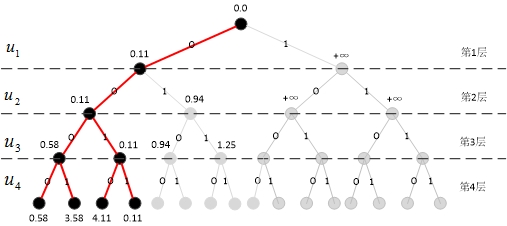
剪枝
到了最后一层,选取PM最小的路径作为唯一路径,即为译码输出结果:\(\hat{u}_{1}^{4}=\left( \begin{matrix} 0 & 0 & 1 & 1 \\ \end{matrix} \right)\)。如图12所示,只保留这一条路径,删除其余路径。
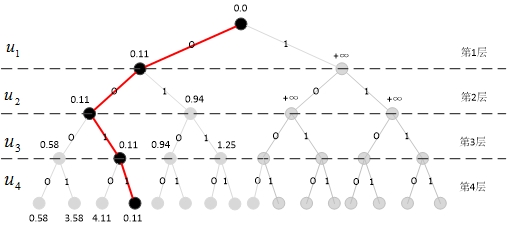
注意,此时的\(\hat{u}_{1}^{4}=\left( \begin{matrix} 0 & 0 & 1 & 1 \\ \end{matrix} \right)\)并不是按正常顺序排列的译码结果。别忘了极化码编码时是经过比特反转的,\(\left( \begin{matrix} 0 & 0 & 1 & 1 \\ \end{matrix} \right)\)对应的比特位置是\(\left( \begin{matrix} 1 & 3 & 2 & 4 \\ \end{matrix} \right)\)。所以再比特反转一次,得到最终的译码比特\(\left( \begin{matrix} 0 & 1 & 0 & 1 \\ \end{matrix} \right)\),其中第2、4位发生了译码错误。
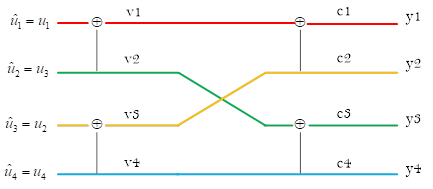
总结
SC译码算法是深度优先的,要的是从根节点快速到达叶子节点。而SCL译码算法是广度优先的,先扩展,再剪枝,最终到达叶子节点。SCL译码算法的PM机制就像“马太效应”,越是错误的路径越要施加惩罚,越是正确的路径越可以直接继承父节点以便保证自己具有最小的PM。对于信息比特且\({ {\hat{u}}_{i}}\left[ l \right]\)与\(\delta \left( L_{N}^{\left( i \right)}\left[ l \right] \right)\)相等的情况,该比特直接继承父节点的PM;对于信息比特且\({ {\hat{u}}_{i}}\left[ l \right]\)与\(\delta \left( L_{N}^{\left( i \right)}\left[ l \right] \right)\)不相等的情况则次之,施加一个惩罚因子,该惩罚因子的大小就是LLR的模值;对于冻结比特而且还取值错误的情况是最坏的,施加的惩罚因子是无穷大。
参考文献
[1] Tal I, Vardy A. List Decoding of Polar Codes[J]. Information Theory IEEE Transactions on, 2012, 61(5):2213-2226. [2] Balatsoukas-Stimming A, Parizi M B, Burg A. LLR-Based Successive Cancellation List Decoding of Polar Codes[J]. IEEE Transactions on Signal Processing, 2015, 63(19):5165-5179. [3] 陈凯. 极化编码理论与实用方案研究[D]. 北京邮电大学, 2014.