Polar Code(8)高斯近似
前言
通过系列文章《Polar Code(1~7)》大致梳理了Polar
Code从编码到译码的基本原理和算法步骤。本文回过头再来谈一谈高斯近似。高斯近似已在前文《Polar
Code(4)编码之极化信道可靠性估计》中有所介绍。对于Polar码的研究从BEC到一般类型的B-DMC,再到BAWGNC,越来越从理想走向实际。密度进化法把BEC扩展到了所有类型的B-DMC,高斯近似法则把B-DMC再次扩展到了BAWGNC。本文将梳理高斯近似在Polar
Code编码和译码中的具体应用。
Polar编码中的高斯近似
高斯近似[1]是对密度进化的简化处理方法,早已广泛应用于LDPC码。高斯近似在Polar
Code编码中用于信道的可靠性估计[2],即估计各个极化信道的错误概率。应用高斯近似法的基本前提是满足对称性条件,因为这正是密度进化法必须满足的条件。如果接收符号对数似然比的概率密度函数满足\(f\left( x \right)=f\left( -x \right){
{e}^{x}}\),那么高斯分布的均值\(m\)和方差\({
{\sigma }^{2}}\)具有如下关系:\({
{\sigma
}^{2}}=2m\)。由于高斯分布本身可以根据其均值和方差完全决定,所以在高斯近似假设条件下,只需要跟踪信息的均值变化就可以知道概率密度的变化。同时定义高斯变量的等效SNR为\({ { {m}^{2}}}/{ { {\sigma
}^{2}}}\;\),所以SNR为\({m}/{2}\;\),跟踪均值也相当于跟踪SNR。
对于方差为\({ {\sigma }^{2}}\)的BAWGN信道\(W\),源比特序列用BPSK调制,其概率密度函数为
\[\begin{align} p\left( y|x \right)=\frac{1}{\sqrt{2\pi { {\sigma }^{2}}}}{ {e}^{-\frac{ { {\left( y-\left( 1-2x \right) \right)}^{2}}}{2{ {\sigma }^{2}}}}} \end{align}\]
接收符号 的对数似然比(LLR)定义为
\[\begin{align} L\left( y \right)=\ln \frac{p\left( y|0 \right)}{p\left( y|1 \right)}=\frac{2y}{ { {\sigma }^{2}}} \end{align}\]
由于此时信道满足了对称性条件,那么译码错误概率与传输的码字无关,因此不失一般性,我们可以假设码字为全零发送,则LLR是服从均值为\(\frac{2}{ { {\sigma }^{2}}}\),方差为\(\frac{4}{ { {\sigma }^{2}}}\)的高斯分布。
高斯近似假设
GA
assumption:每个子信道的LLR都服从方差为均值2倍的高斯分布,即
\[\begin{align} L_{N}^{\left( i \right)}\sim N\left( m_{N}^{\left( i \right)},2m_{N}^{\left( i \right)} \right) \end{align}\]
其中,\(m_{1}^{\left( 1 \right)}=\frac{2}{ { {\sigma }^{2}}}\)。
基于这样的高斯近似假设,唯一需要考虑的问题就是如何计算均值。根据密度进化中的设定,令\(a_{N}^{\left( i \right)}\)表示\(L_{N}^{\left( i \right)}\left( y_{1}^{N},0_{1}^{i-1} \right)\)的概率密度函数,那么\(a_{N}^{\left( i \right)}\)是服从\(N\left( m_{N}^{\left( i \right)},2m_{N}^{\left( i \right)} \right)\)的高斯分布。再根据高斯近似的构造理论,将密度进化的计算转化为对均值\(m_{N}^{\left( i \right)}\)的递归计算:
\[\begin{align} m_{2N}^{\left( 2i\text{-}1 \right)}={ {\varphi }^{-1}}\left( 1-{ {\left[ 1-\varphi \left( m_{N}^{\left( i \right)} \right) \right]}^{2}} \right) \end{align}\]
\[\begin{align} m_{2N}^{\left( 2i \right)}=2m_{N}^{\left( i \right)} \end{align}\]
\[\begin{align} m_{1}^{\left( 1 \right)}={2}/{ { {\sigma }^{2}}}\; \end{align}\]
其中函数
\[\begin{align} \varphi \left( x \right)=\left\{ \begin{matrix} 1-\frac{1}{\sqrt{4\pi x}}\int_{-\infty }^{\infty }{\tanh \frac{u}{2}\cdot \exp \left( -\frac{ { {\left( u-x \right)}^{2}}}{4x} \right)du,x>0} \\ 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0 \\ \end{matrix} \right. \end{align}\]
\(\varphi \left( x \right)\)在\(\left[ 0,\infty \right)\)上连续单调递减,\(\varphi \left( 0 \right)\text{=}1\),\(\varphi \left( +\infty \right)\text{=0}\),其反函数用\({ {\varphi }^{-1}}\left( x \right)\)表示。一般情况下,函数\(\varphi \left( x \right)\)可以使用如下GA近似式(AGA)[1]计算
\[\begin{align} \varphi \left( x \right)=\left\{ \begin{matrix} \sqrt{\frac{\pi }{x}}\left( 1-\frac{10}{7x} \right)\exp \left( -\frac{x}{4} \right),x\ge 10 \\ \exp \left( -0.4527{ {x}^{0.86}}+0.0218 \right),0<x<10 \\ \end{matrix} \right. \end{align}\]
我发现的问题
注意式(8)的第二个式子中0.86应当是个正数,其出处在Sae-Young
Chung于2001年发表的论文[1]中,如图1所示。

许多中文文献虽然同样引用了这篇论文,但$$值却是-0.86。这些使用-0.86的文献不乏最近一两年(2015、2016)的硕博士论文,这里并不一一举例,仅就事论事地指出这个问题可能值得商榷。由于密度进化和高斯近似在LDPC码中早已应用,也可以举一个关于LDPC码早已成书的例子,在2008年出版的《LDPC码理论与应用》[3]一书中,在120页就使用了-0.86,如图2所示。

下面就比较一下0.86和-0.86对\(\varphi \left( x \right)\)函数的影响有何不同,如图2和图3所示。
\(x\ge 10\)的范围是完全相同的;不同的地方就在于\(0<x<10\)。这会影响均值的取值,从而影响LLR的概率密度。这一点很重要,涉及到仿真参数的配置和仿真性能。
关于这一点就说到这里,我的结论是:gamma的取值还是回到Sae-Young Chung的原始论文,取值为正0.86。
改进的AGA
高斯近似是对密度进化的简化,既然是简化,就会以损失一部分性能为代价。幸运的是,这代价很小,是可以接受的范围,如图2所说,高斯近似与密度进化的信道参数极限值仅相差\(0.3%\sim
1.2%\)。但式(7)计算起来稍显复杂,于是Sae-Young
Chung提出了对高斯近似的近似式(Approximate version of
GA,AGA),也就是式(8)。
不过对于Polar Code,当码长\(N\)很长时,由于式(8)的计算误差会带来很大的性能损失,于是Jincheng Dai等人提出了改进的AGA。文献[4]采用累积对数误差(cumulative-logarithmic error,CLE)来定量评估AGA在对数域上的余补误差,提出了新的两段式估计函数
\[\begin{align} { {\varphi }_{AGA-2}}\left( x \right)=\left\{ \begin{matrix} { {e}^{0.0116{ {x}^{2}}-0.4212x}},\ 0<x\le a \\ { {e}^{-0.2944x-0.3169}},\ a<x \\ \end{matrix} \right. \end{align}\]
其中,临界点\(a=7.0633\)。与此同时,还提出了一种适合于Polar Code,特别是对于长码的三段式估计函数
\[\begin{align} { {\varphi }_{AGA-3}}\left( x \right)\text{=}\left\{ \begin{matrix} { {e}^{0.06725{ {x}^{2}}-0.4908x}},\ 0<x\le a \\ { {e}^{-0.4527{ {x}^{0.86}}+0.0218}},\ a<x\le b \\ { {e}^{-0.2832x-0.4254}},\ b<x \\ \end{matrix} \right. \end{align}\]
其中,临界点\(a=0.6357,b=9.2254\)。
通过式(4~6)、式(9)或式(10)即可递归求出各极化信道的均值。
\({ {\varphi }_{AGA-2}}\left( x \right)\)的反函数详见《Answer-Polar Code-高斯近似之\(\varphi \left( x \right)\)反函数》。
极化子信道错误概率
根据式(3)的高斯近似假设,各个极化子信道的错误概率为
\[\begin{align} { {P}_{e}}\left( W_{N}^{\left( i \right)} \right)=Q\left( \frac{m_{N}^{\left( i \right)}}{\sqrt{2m_{N}^{\left( i \right)}}} \right)=Q\left( \sqrt{\frac{m_{N}^{\left( i \right)}}{2}} \right) \end{align}\]
其中\(Q\left( x \right)=\frac{1}{\sqrt{2\pi }}\int_{x}^{+\infty }{ { {e}^{-\frac{ { {t}^{2}}}{2}}}}dt\)为余补误差函数。
至此,高斯近似在Polar Code编码中的使命就完成了。接下来就是《Polar Code(3)编码实例》中的第二步比特混合了。
Polar译码中的高斯近似
在接收端译码时,首先要计算如图5最右端所示的信道对数似然比\(L_{1}^{\left( 1 \right)}\left( { {y}_{j}}
\right)\)。假设接收端的接收序列为\(y_{1}^{N}\),直接由式(2)即可依次计算出:
\[\begin{align} L_{1}^{\left( 1 \right)}\left( { {y}_{j}} \right)=\ln \frac{W\left( y|0 \right)}{W\left( y|1 \right)}=\frac{2{ {y}_{j}}}{ { {\sigma }^{2}}} \end{align}\]
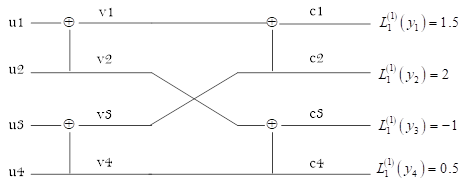
接下来就可以利用LLR递归式依次计算各个节点的LLR值了。
总结
转移概率,多么重要的信道参数。高斯近似,多么重要的估计方法。有了这两点,就可以把Polar
Code编码和译码各个环节串联起来。在编码端,通过高斯近似估计子信道错误概率,扬长避短,择其善者而传信息,避其不善者而冻结。然后比特混合,构造生成矩阵,终成一列极化码。在译码端,还是通过高斯近似估计信道对数似然值,构造判决函数,或深度优先或广度优先,逐比特判决,从而估计出源比特序列。
参考文献
[1] Chung S Y, Richardson T J, Urbanke R L. Analysis of
sum-product decoding of low-density parity-check codes using a Gaussian
approximation[J]. IEEE Transactions on Information Theory, 2001,
47(2):657-670. [2] Trifonov P. Efficient Design and Decoding of Polar
Codes[J]. IEEE Transactions on Communications, 2012, 60(11):3221-3227.
[3] 袁东风, 张海刚. LDPC码理论与应用[M]. 人民邮电出版社, 2008. [4] Dai
J, Niu K, Si Z, et al. Evaluation and Optimization of Gaussian
Approximation for Polar Codes[J]. Proceedings of the American Society
for Information Science & Technology, 2016, 51(1):1-2.