5G-NR物理信道与调制v1.1.0
Marshall:5G NR物理层规范已更新到v1.1.0版本,本文整理了38.211规范v1.1.0版,同时宣告v1.0.0版本过时。

Scope
References
Definitions, symbols and abbreviations
帧结构与物理资源
概述
在本规范中,除非另有说明,时域中各个域的大小表示为若干时间单位\({ {T}_{\text{c}}}={1}/{\left( \Delta { {f}_{\max
}}\cdot { {N}_{\text{f}}} \right)}\;\),其中\(\Delta { {f}_{\max }}=480\cdot { {10}^{3}}\text{
Hz}\),\({
{N}_{\text{f}}}=4096\)。常数\(\kappa ={
{ {T}_{\text{s}}}}/{ { {T}_{\text{c}}}}\;=64\),其中\({ {T}_{\text{s}}}={1}/{\left( \Delta {
{f}_{\text{ref}}}\cdot { {N}_{\text{f,ref}}} \right)}\;\),\(\Delta { {f}_{\text{ref}}}=15\cdot {
{10}^{3}}\text{ Hz}\),\({
{N}_{\text{f,ref}}}=2048\)。
\({ {T}_{\text{s}}}\)是LTE的采样间隔,为了不引起混淆,NR的采样间隔用新的符号\({ {T}_{c}}\)命名,\({ {T}_{c}}=64{ {T}_{s}}\)。
波形参数
如Table 4.2-1所示,NR支持多种OFDM波形参数。部分载波带宽(carrier
bandwidth part)的$
$和CP由高层参数给定,其中下行链路由DL_BWP_mu和DL_BWP_cp给定,上行链路由UL_BWP_mu和UL_BWP_cp给定。
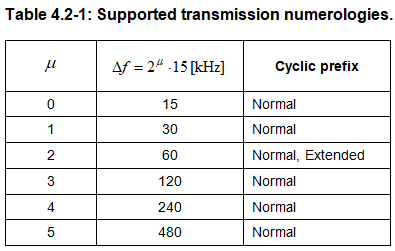
Marshall:NR支持多种子载波间隔,当$ $时即为LTE的参数配置,也就是说LTE的参数配置是NR的一个特例。
帧结构
帧和子帧
下行与上行链路传输于帧中,一帧的时域为$ { {T}{}}=( {}/{100};
)=10 \(,一帧包含10个子帧,每个子帧时域为\) {
{T}{}}=( {}/{1000}; )=1 \(。每个子帧内连续的OFDM符号数为\)
N_{}{,}=N_{}{}N_{}^{,}
$。每帧分为两个相等大小的半帧,每个半帧包含5个子帧,即半帧0由子帧0-4组成,半帧1由子帧5-9组成。
在一个载波上有一组帧用于上行链路,有一组帧用于下行链路。
来自UE的上行帧\(i\)应在UE对应的下行帧开始前$ { {T}{}}={ {N}{}}{ {T}_{}} $传输。
时隙
对于子载波间隔配置$ \(,时隙在子帧内按递增顺序编号为\) n_{}^{}{
0,...,N_{}^{}-1 } \(,在帧内按递增顺序编号为\) n_{}^{}{
0,...,N_{}^{}-1 } \(。一个时隙内有\)
N_{}^{} \(个连续的OFDM符号,其中\)
N_{}^{} \(的值依赖于CP长度,CP长度由Tables
4.3.2-1 and 4.3.2-2给定。一个子帧内的起始时隙\) n_{}^{} \(与这个子帧内起始OFDM符号\)n_{}{}N_{}{}$在时间上对齐。
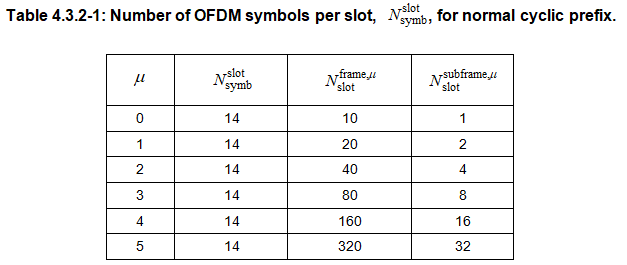

Marshall:一个帧是10ms,一个子帧是1ms,一个子帧内的时隙数是不定的,而一个时隙内的符号数是固定的,因此一个子帧内的符号数是不定的。这里唯一变化的参数就是时隙数,而时隙数是根据子载波间隔配置$ \(来确定的。追溯到源头,是由于\) $的不同配置,带来了上述参数的变化。
物理资源
天线端口
天线端口定义为,在同一个天线端口上,传输某一符号的信道可以从传输另一个符号的信道推知。
若在一个天线端口上传输的某一符号的信道的大尺度特性,可以从另一个天线端口上传输的某一符号的信道推知,则这两个天线端口被称为是准共定位(quasi co-located,QCL)的。大尺度特性包括一个或多个时延扩展,多普勒频移,平均增益,平均时延,空间Rx参数。
资源格
对于给定的波形参数和子载波间隔配置,资源格定义为$
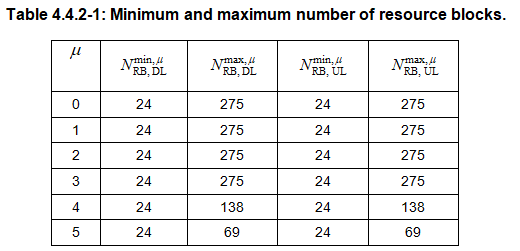
N_{x}{}N_{}{} \(个频域子载波和\) N_{}^{,} \(个时域OFDM符号,其中\) N_{x}^{} \(由Table 4.4.2-1给定,\) x \(表示DL(downlink)或UL(uplink)。在不会产生混淆时,下标\)
x \(可省略。每个天线端口\) p \(、每个子载波间隔配置\)
$以及每个传输方向(上行或下行),对应一个资源格。
资源粒子
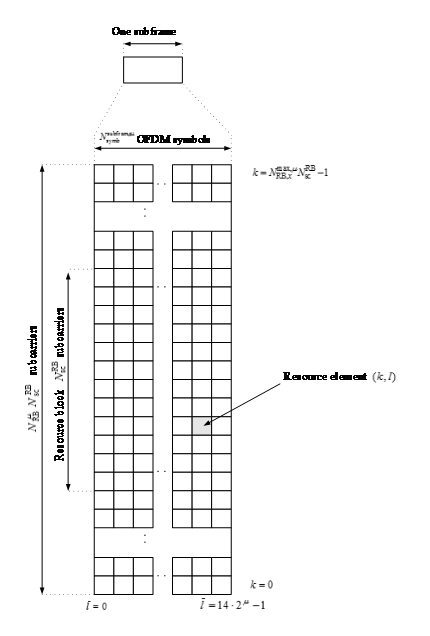
对于天线端口$ p \(和子载波间隔配置\) \(,资源格中的每个元素被称为资源粒子,并且由索引对\)
( k,l ) \(唯一地标识,其中\) k \(是频域索引,\) l $是时域符号索引。
天线端口$ p \(和子载波间隔配置\) \(下的资源粒子表示为\) { {( k,l )}{p,}} \(,其对应的复数值为\) a{k,l}^{(p,)} \(。在不会产生混淆时,或在没有指定某一天线端口或子载波间隔时,索引\) p \(和\) \(可以省略,表示为\) a_{k,l}^{(p)} \(或\) { {a}_{k,l}} $。
一个资源粒子可分为“上行链路”、“下行链路”、“灵活”或“保留”。
- 如果一个资源粒子被配置为“保留”,UE不应在上行链路资源粒子中传输任何数据,也不应假设下行链路资源粒子中有任何内容。
资源块
在频域内,物理资源块定义为$ N_{}^{}=12 $连续的子载波。
在频域内,物理资源块从0到$ N_{}^{}-1 \(进行编号。在频域内,物理资源块号\) { {n}_{}} $与资源粒子 的关系如下:
\[ { {n}_{\text{PRB}}}=\left\lfloor \frac{k}{N_{\text{sc}}^{\text{RB}}} \right\rfloor \]
部分载波带宽
对于给定载波上的给定波形参数$ { {}{i}} \(,部分载波带宽(Carrier bandwidth
part)定义为一个物理资源块(在4.4.4中定义)的连续子集。BWP中的资源块从0到\)
N{x}^{}-1 \(进行编号,其中\) x
\(表示DL(downlink)或UL(uplink)。\)
N_{}^{i} \(是4.4.4节中绝对资源块格栅中的PRB0与编号为\)i\(的部分载波载波带宽中的PRB0之间的偏移。一个BWP内的资源块数应满足\)
N_{x}{}N_{x}{}N_{x}^{} $,其中最小与最大值由Table
4.4.2-1给定。
在下行链路,UE可以配置一个或多个BWP,并且可以在指定的时间对下行BWP进行激活。在激活的BWP之外,UE不会接收PDSCH或PDCCH。
在上行链路,UE可以配置一个或多个BWP,并且可以在指定的时间对上行BWP进行激活。在激活的BWP之外,UE不会接收PUSCH或PUCCH。
载波聚合
多个小区的传输可以被聚合起来,除了主小区之外最多可聚合15个次级小区。除非另有说明,本规范中的描述适用于多达16个服务小区中的每一个。
通用函数
调制映射器
调制映射器采用二进制0或1作为输入,产生复值调制符号作为输出。
π/2-BPSK
对于π/2-BPSK调制,比特\(b(i)\)根据下式映射为复值调制符号\(x\)
\[x=\frac{ { {e}^{j{i\pi }/{2}\;}}}{\sqrt{2}}\left[ \left( 1-2b(i) \right)+j\left( 1-2b(i) \right) \right]\]
BPSK
对于BPSK调制,比特\(b(i)\)根据下式映射为复值调制符号\(x\)
\[x=\frac{1}{\sqrt{2}}\left[ \left( 1-2b(i) \right)+j\left( 1-2b(i) \right) \right]\]
QPSK
对于QPSK调制,成对比特\(b(i),b(i+1)\)根据下式映射为复值调制符号\(x\)
\[x=\frac{1}{\sqrt{2}}\left[ \left( 1-2b(i) \right)+j\left( 1-2b(i+1) \right) \right]\]
16QAM
对于16QAM调制,四位比特\(b(i),b(i+1),b(i+2),b(i+3)\)根据下式映射为复值调制符号\(x\)
\[x=\frac{1}{\sqrt{10}}\left[ \left( 1-2b(i) \right)\left( 2-\left( 1-2b(i+2) \right) \right)+j\left( 1-2b(i+1) \right)\left( 2-\left( 1-2b(i+3) \right) \right) \right]\]
64QAM
对于64QAM调制,六位比特\(b(i),b(i+1),b(i+2),b(i+3),b(i+4),b(i+5)\)根据下式映射为复值调制符号\(x\)
\[\begin{align} \nonumber & x=\frac{1}{\sqrt{42}}\left[ \left( 1-2b(i) \right)\left( 4-\left( 1-2b(i+2) \right)\left( 2-\left( 1-2b(i+4) \right) \right) \right) \right. \\ \nonumber & \ \ \ \ \ \ \left. +j\left( 1-2b(i+1) \right)\left( 4-\left( 1-2b(i+3) \right)\left( 2-\left( 1-2b(i+5) \right) \right) \right) \right] \\ \end{align}\]
256QAM
对于256QAM调制,八位比特\(b(i),b(i+1),b(i+2),b(i+3),b(i+4),b(i+5),b(i+6),b(i+7)\)根据下式映射为复值调制符号\(x\)
\[\begin{align} \nonumber & x=\frac{1}{\sqrt{170}}\left[ \left( 1-2b(i) \right)\left( 8-\left( 1-2b(i+2) \right)\left( 4-\left( 1-2b(i+4) \right)\left( 2-\left( 1-2b(i+6) \right) \right) \right) \right) \right. \\ \ \ \ \nonumber & \left. +j\left( 1-2b(i+1) \right)\left( 8-\left( 1-2b(i+3) \right)\left( 4-\left( 1-2b(i+5) \right)\left( 2-\left( 1-2b(i+7) \right) \right) \right) \right) \right] \end{align}\]
序列生成
伪随机序列生成
伪随机序列由长度为31的Gold序列定义。输出序列$ c(n) \(长度为\) { {M}{}} \(,其中\) n=0,1,...,{ {M}{}}-1 \(,\) c(n) $由下式定义
\[ \begin{align} \nonumber & c(n)=\left( { {x}_{1}}(n+{ {N}_{C}})+{ {x}_{2}}(n+{ {N}_{C}}) \right)\bmod 2 \\ \nonumber & { {x}_{1}}(n+31)=\left( { {x}_{1}}(n+3)+{ {x}_{1}}(n) \right)\bmod 2 \\ \nonumber & { {x}_{2}}(n+31)=\left( { {x}_{2}}(n+3)+{ {x}_{2}}(n+2)+{ {x}_{2}}(n+1)+{ {x}_{2}}(n) \right)\bmod 2 \end{align} \]
其中$ { {N}{C}}=1600 \(,第一m序列应由\) { {x}{1}}(0)=1,{ {x}{1}}(n)=0,n=1,2,...,30 \(初始化。第二m序列由\) { {c}{}}={i=0}^{30}{ { {x}{2}}(i)} $进行初始化,其值取决于序列的应用。
ZC序列生成
序列$ r_{u,v}^{(,)}(n) \(由基序列\) { _{u,v}}(n) \(根据下式的循环移位\) $得到:
\[ r_{u,v}^{(\alpha ,\delta )}(n)=\begin{matrix} { {e}^{j\alpha \left( n+\delta \frac{\omega \bmod 2}{2} \right)}}{ { {\bar{r}}}_{u,v}}(n), & 0\le n<{ {M}_{\text{ZC}}} \\ \end{matrix}-1 \]
其中$ { {M}{}}={mN{}^{}}/{ { {2}^{}}}; \(是序列长度,且\) 1mN_{}^{} \(。多个序列由基序列根据不同的\) \(和\) $值来得到。
基序列$ { {u,v}}(n) \(被分为若干组,\) u{ 0,1,...,29 } \(是分组号,\) v \(是组内基序列号。每个组包含一个长度为\) { {M}{}}=mN_{}^{} \(的基序列(\) v=0 \()且\) 1m \(,和两个长度为\) { {M}{}}=mN{}^{} \(的基序列(\) v=0,1 \()且\) 6mN_{}^{} \(。基序列\) { {u,v}}(0),...,{ {u,v}}({ {M}{}}-1) \(的定义依赖于序列长度\) { {M}{}} $。
长度大于等于$ 3N_{}^{} $的基序列
对于$ { {M}{}}3N{}^{} \(,基序列\) { {u,v}}(0),...,{
{u,v}}({ {M}_{}}-1) $为
\[ \begin{align} \nonumber & { { {\bar{r}}}_{u,v}}(n)={ {x}_{q}}\left( n\bmod { {N}_{\text{ZC}}} \right) \\ \nonumber & { {x}_{q}}\left( m \right)={ {e}^{-j\frac{\pi qm\left( m+1 \right)}{ { {N}_{\text{ZC}}}}}} \end{align} \]
其中
\[ \begin{align} \nonumber & q=\left\lfloor \bar{q}+{1}/{2}\; \right\rfloor +v\cdot { {(-1)}^{\left\lfloor 2\bar{q} \right\rfloor }} \\ \nonumber & \bar{q}={ {N}_{\text{ZC}}}\cdot {(u+1)}/{31}\; \\ \end{align} \]
长度$ { {N}{}} \(为满足\) { {N}{}}<{ {M}_{}} $的最大素数。
长度小于$ 3N_{}^{} $的基序列
对于$ { {M}{}}={ {N}{}} \(和\) { {M}{}}=2{ {N}{}}
$,基序列为
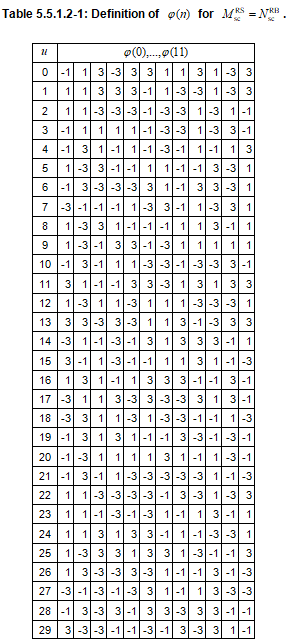
\[ { {\bar{r}}_{u,v}}(n)=\begin{matrix} { {e}^{j{\phi (n)\pi }/{4}\;}}, & 0\le n\le { {M}_{\text{ZC}}}-1 \\ \end{matrix} \]
其中$ (n) $的值由Tables 5.5.1.2-1 and 5.5.1.2-2给定。

OFDM基带符号生成
时域连续序号$ s_{l}^{(p,)}( t ) \(是天线端口\) p \(和子载波间隔配置\) \(下,在一个子帧内的第\) l
$个OFDM符号。OFDM符号用于除PRACH之外的任何物理信道或物理信号,定义为
\[ s_{ {\bar{l}}}^{(p,\mu )}\left( t \right)=\sum\limits_{k=-\left\lfloor N_{\text{RB}}^{\mu }N_{\text{sc}}^{\text{RB}}/2 \right\rfloor }^{ { {\left\lceil N_{\text{RB}}^{\mu }N_{\text{sc}}^{\text{RB}}/2 \right\rceil }^{ {}}}-1}{a_{ {k}',l}^{(p,\mu )}\cdot { {e}^{j2\pi \left( k+{ {k}_{0}} \right)\Delta f\left( t-{ {N}_{\text{CP},l}}{ {T}_{\text{c}}} \right)}}} \]
其中$ 0t<( { {N}{}}+N{,{l}}^{} ){ {T}{}} \(且\) {k}'=k+/{2}; \(。\) { {k}{0}} \(是在子载波间隔配置\) \(下,一个RB内最低编号的子载波,并且与任何小于\) $的配置下的RB内最低编号的子载波相一致。
子载波间隔配置$ \(下,一个子帧内OFDM符号\) l $的起始位置为
\[ t_{\text{start},l}^{\mu }=\left\{ \begin{array}{*{35}{l}} 0 & l=0 \\ t_{\text{start},l-1}^{\mu }+\left( { {N}_{\text{u}}}+N_{\text{CP,}l-1}^{\mu } \right)\cdot { {T}_{\text{c}}} & \text{otherwise} \\ \end{array} \right. \]
其中
\[ \begin{align} \nonumber & { {N}_{\text{u}}}=2048\kappa \cdot { {2}^{-\mu }} \\ \nonumber & { {N}_{\text{CP},l}}=\left\{ \begin{array}{*{35}{l}} 512\kappa \cdot { {2}^{-\mu }} & \text{extended cyclic prefix} \\ 144\kappa \cdot { {2}^{-\mu }}+16\kappa & \text{normal cyclic prefix and }l=0\text{ or }l=7 \\ 144\kappa \cdot { {2}^{-\mu }} & \text{otherwise} \\ \end{array} \right.\cdot { {2}^{\mu }} \end{align} \]
时域连续符号$ s_{l}^{(p,)}( t ) \(是天线端口\) p $上用于传输PRACH的符号,定义为
\[ s_{l}^{(p,\mu )}\left( t \right)=\sum\limits_{k=-\left\lfloor { {L}_{\text{RA}}}/2 \right\rfloor }^{ { {\left\lceil { {L}_{\text{RA}}}/2 \right\rceil }^{ {}}}-1}{a_{ { {k}'}}^{(p,\text{RA})}\cdot { {e}^{j2\pi \left( k+{ {k}_{0}} \right)\Delta { {f}_{\text{RA}}}\left( t-N_{\text{CP},l}^{\text{RA}}{ {T}_{\text{c}}} \right)}}} \]
其中$ 0t<( { {N}{}}+N{,l}^{} ){ {T}_{}} \(且\) {k}'=k+/{2}; $。
一个子帧内PRACH前导的起始位置定义为$ t_{}^{} \(,假设子帧在\) t=0 $时刻开始,
- 对于$ { 15,30,60,120 } \(,对于符号\) l \(有\) t_{}{}=t_{,l}{} $
$ { {L}{}} \(和\) { {N}{}} \(由6.3.3节和\) N_{,l}{}=N_{}{}+n$给定,其中
- 对于$ { 1.25,5 } \(,有\) n=0 $
- 对于$ { 15,30,60,120 } \(,\)n$ is the number of times the interval $ $ overlaps with either time instance 0 or time instance $ ( {}/{2000}; )=0.5 $ in a subframe.
调制和上变频
对于天线端口$ p \(和子载波间隔配置\) \(,复值OFDM基带信号调制和上变频至载频\) {
{f}_{0}} $:
\[ \operatorname{Re}\left\{ s_{l}^{(p,\mu )}\left( t \right)\cdot { {e}^{j2\pi { {f}_{0}}t}} \right\} \]