Polar Code(13)信道极化
1、 信道极化是一种现象,把它看作一种原理,而极化码编码则是对这一原理的应用。理解极化码可以分两部分,一部分是理论,一部分是应用。
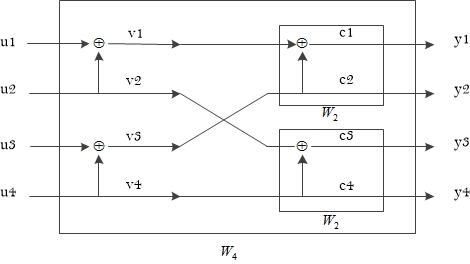
2、 从图上看,信道极化过程是一目了然的。但从数学上看,信道极化要分两个阶段,第一阶段是信道联合,第二阶段就是信道分裂。信道分裂是信道极化的一部分。
3、 信道极化作为一种原理,它也有它的结构。它的结构就是:原本\(N\)条平行线,互不相交,谁和谁都没有联系,换句话说,是\(N\)条原始信道的独立副本;经过各种连线、模二加,连来连去,连成了现在的样子;现在是\(N\)条线彼此都有联系。这个过程就是信道联合,把原本相互独立的\(N\)条细线扭成一条粗线。
4、 信道联合是从宏观的角度观察,把信道极化过程看作一个整体,输入是\(N\)比特,输出也是\(N\)比特。经过联合的信道总是以整体的形式表达,如联合信道\({ {W}_{4}}:{ {X}^{4}}\to { {Y}^{4}}\),以及联合信道的转移概率\({ {W}_{4}}\left( y_{1}^{4}|u_{1}^{4} \right)\)。
5、 但只有信道联合是不够的,你无法确知各个子信道的输入和输出是什么关系。这就需要对信道极化过程有一个微观的表达,这个微观表达是通过信道分裂过程来实现的。到信道联合这一步还看不出“极化”的概念,必须经过信道分裂才能体现出极化现象。
6、 信道分裂使已经扭成一条粗线的联合信道又重新一条一条地展现在世人面前,就好比两条绳子打结(信道联合),然后再区分出两端谁是谁(信道分裂)。经过分裂的信道总是以单个的形式表达,如分裂子信道\(W_{N}^{\left( i \right)}:X\to { {Y}^{N}}\times { {X}^{i-1}}\),以及分裂子信道的转移概率\(W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}} \right)\)。
7、 宏观和微观合在一起就构成了对信道极化过程的完整表达。我们的目的不只是观其大概,更要搞清楚各个子信道,求分裂子信道的转移概率。《Polar Code(12)B-DMC对称容量》一文中提到,输入符号概率、输出符号概率和转移概率完整地定义了一种信道。不搞清楚各分裂子信道的转移概率就无法完成对分裂信道的定义。从以下定义式就可以看出联合信道和分裂子信道的关系了:
\[\begin{align} W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{ {u}_{i}} \right)\triangleq \sum\limits_{u_{i+1}^{N}\in { {X}^{N-i}}}{\frac{1}{ { {2}^{N-1}}}{ {W}_{N}}\left( y_{1}^{N}|u_{1}^{N} \right)} \end{align}\]
8、 但式(1)是不易求的。观察图1,整个信道极化过程恰好是一种递归形式。因此用两个递归式来计算各个分裂子信道的转移概率:
\[\begin{align} W_{N}^{\left( 2i-1 \right)}\left( y_{1}^{N},u_{1}^{2i-2}|{ {u}_{2i-1}} \right)=\sum\limits_{ { {u}_{2i}}}{\frac{1}{2}W_{ {N}/{2}\;}^{\left( i \right)}\left( y_{1}^{ {N}/{2}\;},u_{1,o}^{2i-2}\oplus u_{1,e}^{2i-2}|{ {u}_{2i-1}}\oplus { {u}_{2i}} \right)\cdot W_{ {N}/{2}\;}^{\left( i \right)}\left( y_{ {N}/{2}\;+1}^{N},u_{1,e}^{2i-2}|{ {u}_{2i}} \right)} \end{align}\]
\[\begin{align} W_{N}^{\left( 2i \right)}\left( y_{1}^{N},u_{1}^{2i-1}|{ {u}_{2i}} \right)=\frac{1}{2}W_{ {N}/{2}\;}^{\left( i \right)}\left( y_{1}^{ {N}/{2}\;},u_{1,o}^{2i-2}\oplus u_{1,e}^{2i-2}|{ {u}_{2i-1}}\oplus { {u}_{2i}} \right)\cdot W_{ {N}/{2}\;}^{\left( i \right)}\left( y_{ {N}/{2}\;+1}^{N},u_{1,e}^{2i-2}|{ {u}_{2i}} \right) \end{align}\]
9、 求得各个分裂子信道的转移概率有什么用?在实际编译码中并没有直接用。当我在3月12日那个时间点上写《Polar Code(5)编码之信道转移概率》的时候,认为转移概率是有用的,并且认为在编码端和译码端都会直接使用,至少对于BEC信道计算巴氏参数时会直接使用。但随着研究的深入,尤其在研究了密度进化和高斯近似之后,对此的认识得到了更新:
- 转移概率是有用的,但并不直接使用,而是使用两个转移概率的之比的对数,即对数似然比(LLR);
- 高斯近似法令转移概率为服从高斯分布的随机变量,并使用对数似然比,直接规避了计算(2)式和(3)式,所以转移概率的两个式子就沦为了铺路者;
- 但式(2~3)的递归形式是十分有用的,译码时计算LLR就利用这种递归形式。
有关高斯近似详见《Polar Code(8)高斯近似》,而《Polar Code(5)编码之信道转移概率》通过分析转移概率的计算过程也能更好的理解编码过程。
10、 编码。极化码是对信道极化原理的应用。然而编码过程又是基于另一套思路,它沿着线性分组码的编码思路,用生成矩阵的方式产生极化码。而生成矩阵的构造又体现着信道极化的原理,用递归形式来构造生成矩阵。
书不尽言,言不尽意。以上几点,是我对信道极化的理解。