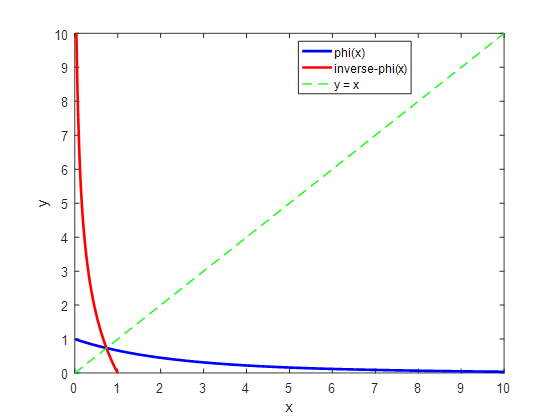
Answer-Polar Code-高斯近似之$\varphi \left( x \right)$反函数
前言
《Polar
Code(8)高斯近似》中\(\varphi \left( x
\right)\)的反函数,计算式(8)比较困难,而式(9)、式(10)比较容易。本文以式(9)为例详述\(\varphi \left( x \right)\)的反函数。
\[\begin{align} { {\varphi }_{AGA-2}}\left( x \right)=\left\{ \begin{matrix} { {e}^{0.0116{ {x}^{2}}-0.4212x}},\ 0<x\le 7.0633 \\ { {e}^{-0.2944x-0.3169}},\ x>7.0633 \\ \end{matrix} \right. \end{align}\]
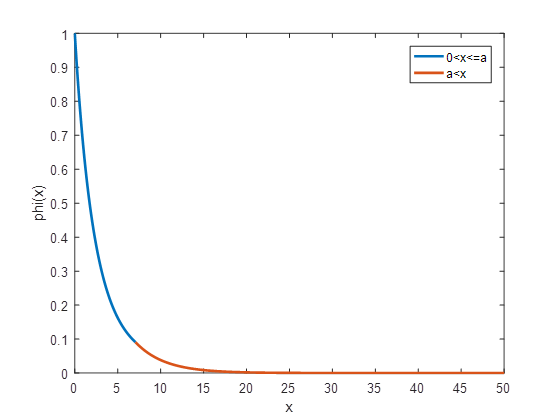
$ { {y}_{1}}={ {e}^{0.0116{ {x}^{2}}-0.4212x}},x( 0,7.0633 ] $的反函数
\[\begin{align} \ln { {y}_{1}}=0.0116{ {x}^{2}}-0.4212x \end{align}\]
\[\begin{align} 0.0116{ {x}^{2}}-0.4212x-\ln { {y}_{1}}=0 \end{align}\]
一元二次方程的根为
\[\begin{align} x=\frac{-b\pm \sqrt{ { {b}^{2}}-4ac}}{2a}=\frac{0.4212\pm \sqrt{ { {0.4212}^{2}}+4\times 0.0116\times \ln { {y}_{1}}}}{2\times 0.0116} \end{align}\]
其中\(a=0.0116,b=-0.4212,c=-\ln { {y}_{1}}\),而$$的选取要做一番比较:
\[\begin{align} \sqrt{ { {b}^{2}}-4ac}=\sqrt{ { {0.4212}^{2}}+4\times 0.0116\times \ln { {y}_{1}}} \end{align}\]
根据定义域$ x( 0,7.0633 ] \(,得到\){ {y}{1}}\(的值域\){ {y}{1}}$的范围,所以“+”号不可取。
若取“-”号,则有
\[0<\frac{-b-\sqrt{ { {b}^{2}}-4ac}}{2a}\le 7.0633\]
此时方程根恰好满足$ x( 0,7.0633 ] $,所以应取“-”号。
综上所述,一元二次方程(3)的根为
\[ \begin{align} x=\frac{-b-\sqrt{ { {b}^{2}}-4ac}}{2a}=\frac{0.4212-\sqrt{ { {0.4212}^{2}}+4\times 0.0116\times \ln { {y}_{1}}}}{2\times 0.0116} \end{align}\]
即反函数为
\[ \begin{align} { {\varphi }^{-1}}\left( x \right)=\frac{0.4212-\sqrt{ { {0.4212}^{2}}+4\times 0.0116\times \ln y}}{2\times 0.0116},y\in \left[ \text{0}\text{.0911},1 \right) \end{align}\]
$ { {y}_{2}}={ {e}^{-0.2944x-0.3169}},x( 7.0633,+) $的反函数
根据$ x( 7.0633,+) \(,得到\){
{y}{2}}\(的值域\){ {y}{2}}(
)$。
\[ \begin{align} \ln { {y}_{2}}=-0.2944x-0.3169 \end{align}\]
\[ \begin{align} x=-\frac{\ln { {y}_{2}}+0.3169}{0.2944} \end{align}\]
即反函数
\[ \begin{align} { {\varphi }^{-1}}\left( x \right)=-\frac{\ln y+0.3169}{0.2944},y\in \left( \text{0,0}\text{.0911} \right) \end{align}\]
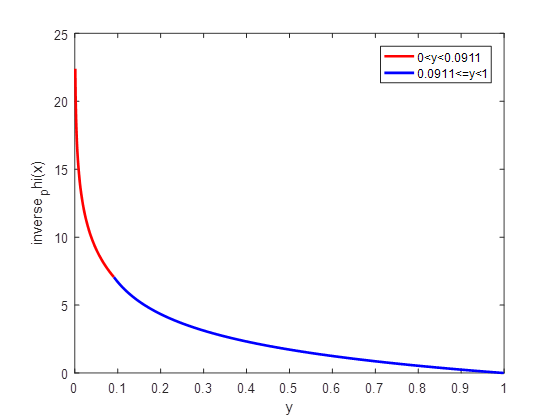
将两段反函数合并得到\(\varphi \left( x \right)\)的反函数
\[ \begin{align} { {\varphi }^{-1}}\left( x \right)=\left\{ \begin{matrix} -\frac{\ln y+0.3169}{0.2944},y\in \left( \text{0,0}\text{.0911} \right) \\ \frac{0.4212-\sqrt{ { {0.4212}^{2}}+4\times 0.0116\times \ln y}}{2\times 0.0116},y\in \left[ \text{0}\text{.0911},1 \right) \\ \end{matrix} \right. \end{align}\]
验证\(\varphi \left( x \right)\)和\({ {\varphi }^{-1}}\left( x \right)\)是否关于y=x对称