Polar Code(20)Beta-expansion
前言
高斯近似(GA)终将成为历史,取而代之的是β-expansion算法。β-expansion与GA性能等价,但复杂度极低。
文献[1]首先揭示了极化码合成信道(synthesized channels)之间的偏序(Partial Order,PO)关系。2016年8月22-26日,在瑞典哥德堡举行的3GPP RAN1 #86次会议上,华为提出了用极化权重(Polarization Weight,PW)来表征AWGN信道下极化码合成信道可靠性的算法[2]。这两项独立的研究似乎不谋而合,促使华为进一步进行理论扩展,追求AWGN信道下极化码的快速构造方法。这就是本博文所要介绍的β-expansion[3]。
文献[3]首先介绍了通用偏序(Universal Partial Order,UPO)的两个重要性质:嵌套和对称。这两个性质是能够采用递归方式构造极化码序列的基础。然后介绍了PW方法,其中β参数需要慎重地选择,其值的大小直接决定了合成信道的顺序。最后用大量的篇幅论证了β的最佳取值为1.1892,即\(\beta ={ {2}^{ {1}/{4}\;}}\)。无论是渐进性分析,还是数值仿真结果都证实β-expansion方法以低复杂度获得了与GA相同的性能。
预备知识
极化码策略
策略:将信息比特放置于好的信道位置上,将冻结比特放置于差的信道位置上。
关键:如何有效地识别信道位置的好坏并按可靠性排序,是极化码序列构造的关键。
不幸:有效地序列构造仅存在于二进制删除信道(BEC)上。
挑战:5G无线通信系统要求极化码至少能够适用于AWGN信道。
已有方法:高斯近似(GA)。
已有方法缺点:GA的缺点是计算量大,其计算量随着码块长度成比例增加,这对于码长和码率变化的实际系统是不可接受的。不仅如此,对于低延迟的编译码器,也无法实现在线地处理。
通用偏序(UPO)
文献[1]证明了任意二进制输入对称信道下的可靠性测量存在偏序(Partial
Order)关系。给定一对合成信道索引\(\left( x,y
\right)\),它们的可靠性关系取决于下列规则:
Addition:若一个合成信道索引用二进制表示为\(\left( a,b,1,c \right)\),那么它的可靠性一定大于合成信道\(\left( a,b,0,c \right)\)。\(''1\succ 0''\)模式对于1比特或多比特同样适用。例如:
2(0, 1 ,0) $$ 3(0, 1, 1)
9(1, 0, 0, 1) $$ 15(1, 1, 1, 1)
在此例中(1, 0, 0, 1)是合成信道索引9的二进制表示。
Left-swap:若合成信道索引为\(\left( a,0,b,1,c \right)\),那么它的可靠性一定小于合成信道\(\left( a,1,b,0,c \right)\)。\(''0...1\prec 1...0''\)模式可以出现多次,并且0,1不需要彼此相邻。例如:
2(0, 1 ,0) $$ 4(1, 0, 0)
12(0, 1, 1, 0, 0) $$ 24(1, 1, 0, 0, 0)
但这两个规则也不是万能的,对于某些索引对\(\left( x,y \right)\)则无能为力。Addition、Left-swap或它们的联合都不能确定顺序。例如:
3(0, 1, 1)and 4(1, 0, 0)
7(0, 1, 1, 1)and 12(1, 1, 0, 0)
我们称这些序对于UPO是未知的。
UPO的性质
Proposition 1.
(嵌套和对称)极化码通用偏序有两个重要性质:
嵌套:码长为\(N\)的序可在码长为\(2N\)的序中保持不变。
对称:在码长为\(N\)的极化码中,\(x\prec y\)的序和\(\left( N-1-x \right)\prec \left( N-1-y \right)\)的序对称。
现在讨论UPO的递归结构。定义\(\mathbf{UP}{ {\mathbf{O}}_{n}}\)为极化码码长\(N\)的偏序关系\(x\prec y\)的最小集合,其中\(x\prec y\)记为\(\left\{ x,y \right\}\),\(x,y\)是\(\left[ 0,N-1 \right]\)内的整数。关系链\(x\prec y\prec z\)可以用若干子链表示最临近节点之间的关系,即\(x\prec y\)和\(y\prec z\)。例如:

其中\(\mathbf{UP}{ {\mathbf{O}}_{n}}\)中黑色字体的序来源于它的上一级\(\mathbf{UP}{ {\mathbf{O}}_{n-1}}\),对应于Proposition 1的嵌套性质;蓝色字体的序表示与黑色字体的序对称的部分,对应于Proposition 1的对称性质;红色字体的序表示从\(\mathbf{UP}{ {\mathbf{O}}_{n-1}}\)到\(\mathbf{UP}{ {\mathbf{O}}_{n}}\)构造过程中出现的新序,这些新出现的序对于UPO来说是未知的。
β-expansion:PW算法原理
定义:(PW 算法)考虑一个合成信道索引\(x\),其\(n\)比特二进制扩展为\(B=\left( { {b}_{n-1}},...,{ {b}_{1}},{ {b}_{0}}
\right)\),最左边为最高有效位。极化权重定义为
\[\begin{align} { {f}^{PW}}:x\mapsto \sum\limits_{i=1}^{n}{ { {b}_{i}}{ {\beta }^{i}}} \end{align}\]
其中$\(的值需要慎重选择。文献[2]建议\)={ {2}^{ {1}/{4};}}$。
在数学上,这种表示方法被称为β-expansion,是十进制扩展的推广,可以看作是对于任意实数\(y\)的基于β的非整数表示。
例1:令\(\beta ={ {2}^{ {1}/{4}\;}}\),极化码码长为\(N={ {2}^{n}}=16\)。则对于合成信道索引3,即\({ {B}_{3}}=\left( 0,0,1,1 \right)\),其β-expansion可计算为
\[{ {w}_{3}}=0\cdot { {2}^{ {3}/{4}\;}}+0\cdot { {2}^{ {2}/{4}\;}}+1\cdot { {2}^{ {1}/{4}\;}}+1\cdot { {2}^{ {0}/{4}\;}}=2.189\cdot \cdot \cdot \]
同理,我们可以写出所有合成信道的β-expansion
\[\begin{align} \nonumber & w=\left\{ \begin{matrix} 0.000 & 1.000 & 1.189 & 2.189 & 1.414 & 2.414 & 2.603 & 3.603 \\ \end{matrix} \right. \\ \nonumber & \ \ \ \ \ \ \ \left. \begin{matrix} 1.682 & 2.682 & 2.871 & 3.871 & 3.096 & 4.096 & 4.285 & 5.285 \\ \end{matrix} \right\} \\ \end{align}\]
\({ {w}_{x}}\)值越大表示合成信道索引\(x\)的可靠性越高。将\(w\)按可靠性增序排列,就得到了极化码序列
\[order=\left\{ \begin{matrix} 0 & 1 & 2 & 4 & 8 & 3 & 5 & 6 & 9 & 10 & 12 & 7 & 11 & 13 & 14 & 15 \\ \end{matrix} \right\}\]
PW算法的优点是,对合成信道可靠性,提供了一种简洁、低复杂度的全排列算法,并且当码长\({ {2}^{n}}\)从\(n=1\)到$n+$增加时,能够始终保持一种嵌套性质。
Proposition 2. (嵌套结构)PW算法维持了极化码的嵌套码构造的特性。
Proposition 3. 当\(\beta >1\),任何由PW算法得到的序列都遵循极化码的通用偏序(UPO)关系。
Theorem 1. 对于长度为\({ {2}^{n}}\left( n\ge 3 \right)\)的极化码,存在一个升序集合\({ {A}_{n}}=\left\{ { {a}_{0}},{ {a}_{1}},{ {a}_{2}},...,{ {a}_{ { {i}_{\max }}}},+\infty \right\}\),其中\({ {a}_{0}}=1\)和\({ {a}_{1}},{ {a}_{2}},...,{ {a}_{ { {i}_{\max }}}}\)都是代数。任意$\(落入区间\)( { {a}{i}},{ {a}{i+1}} ),i\(内,β-expansion都是唯一的,并且\)\(落入不同区间可导致不同的顺序序列。此外,集合\){ {A}{n}}\(是嵌套的,即\){ {A}{n}}$。
Marshall:通过上述Proposition和Theorem,初步地把β-expansion和偏序建立起联系,β-expansion获得了偏序的理论支撑。两者的共性在于,它们都具有嵌套结构。然而$$的值究竟取何值呢?这还需要在具体的用例中去分析和确定。
AWGN信道下的快速构造
现在UPO已经成为极化码序列构造的基础,而极化码序列的构造决定了合成信道的可靠性顺序。但UPO无法做到对整个序列进行全排列,正如在UPO的性质一节所看到的,从\(\mathbf{UP}{ {\mathbf{O}}_{n-1}}\)到\(\mathbf{UP}{
{\mathbf{O}}_{n}}\)的构造中,总会有一些新的序是UPO无法判断的。而高斯近似虽然能够对整个序列进行全排序,但由于其高复杂度而不适用于实际应用。为了克服两者的缺点,本节呈现了一种基于UPO和β-expansion的快速构造方法。
Marshall:根据高斯近似的结果,一步一步缩小$$的取值范围,最终的序列不仅满足UPO性质,而且与高斯近似的结果保持一致。换句话说,没有条件,就去创造条件。
解释一下为什么$$的取值会影响序列顺序,如图1所示。
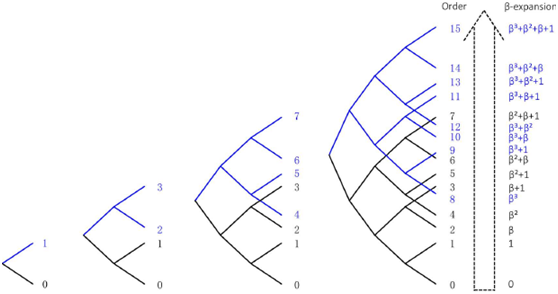
根据定理1,是默认为\(\beta >1\),所以今后只考虑\(\beta >1\)。
当\(n=3\)时,只有一对未定关系,即\(\left( \beta +1,{ {\beta }^{2}} \right)\)。为了区分它们的关系,需要多项式方式\({ {x}^{2}}-x-1=0\),取其大于1的根为\(x=\frac{1+\sqrt{5}}{2}=1.618\),因此升序集合为
\[{ {A}_{3}}=\left\{ 1,1.618,+\infty \right\}\]
当\(\beta \in \left( 1,1.618 \right)\)时,有\(\beta +1>{ {\beta }^{2}}\),则相应的序列为

当\(\beta \in \left( 1.618,+\infty \right)\)时,有\(\beta +1<{ {\beta }^{2}}\),则相应的序列为

这就是定理1所说的,当$\(落入\){ {A}_{3}}$的任意区间内,β-expansion是唯一的,且导致不同的顺序序列。
当\(n=4\)时,有4对未定关系,包括之前提到的\(\left( \beta +1,{ {\beta }^{2}} \right)\)及其两个等价形式,即
\[\begin{align} \nonumber & \left( \beta +1,{ {\beta }^{2}} \right),\left( { {\beta }^{2}}+\beta ,{ {\beta }^{3}} \right),\left( { {\beta }^{2}}+\beta ,{ {\beta }^{3}} \right) \\ \nonumber & \left( \beta +1,{ {\beta }^{3}} \right),\left( { {\beta }^{2}}+1,{ {\beta }^{3}} \right),\left( { {\beta }^{2}}+\beta +1,{ {\beta }^{3}} \right) \\ \end{align}\]
为了区分它们的关系,需要求解4个多项式方程
\[\begin{align} { {x}^{3}}-{ {x}^{2}}-x-1=0 \end{align}\]
\[\begin{align} { {x}^{3}}-{ {x}^{2}}-1=0 \end{align}\]
\[\begin{align} { {x}^{2}}-x-1=0 \end{align}\]
\[\begin{align} { {x}^{3}}-x-1=0 \end{align}\]
得到
\[{ {A}_{4}}=\left\{ 1,1.325,1.466,1.618,1.839,+\infty \right\}\]
其中1.325,1.466,1.618,1.839分别是多项式方程(2~5)的根。
$\(分别落入\){ {A}_{4}}$的5段子区间内,将导致5种不同的序,如图2所示。
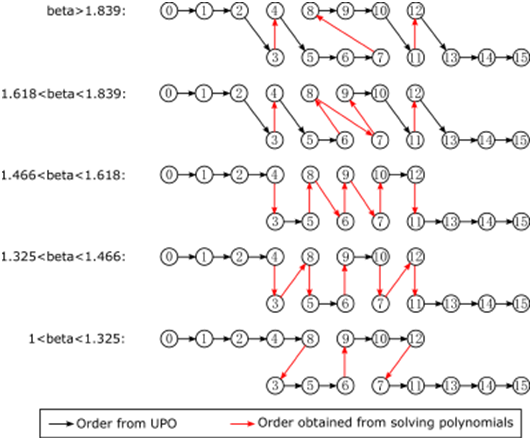
$\(取哪个值?此时高斯近似法开始派上用场。对于码长\)N={ {2}^{4}}=16\(,\)n=4$的极化码,AWGN信道下,高斯近似法对合成信道索引的排序为
\[\begin{align} \nonumber & 0\to 1\to 2\to 4\to 8\to 3\to 5\to 6\to 9 \\ \nonumber & \to 10\to 12\to 7\to 11\to 13\to 14\to 15 \\ \end{align}\]
将这个序与图2对比,发现当\(\beta \in \left( 1,1.325 \right)\)时,两个序一致。
由此,我们将$\(的取值范围由\)n=3\(时的\)( 1,1.618 )\(缩小到\)n=4\(时的\)( 1,1.325 )$。
进一步,当\(n=5\)时,有5对未定关系,即\(\left( 28,15 \right),\left( 14,19 \right),\left( 24,13 \right),\left( 24,11 \right),\left( 24,7 \right)\)。根据高斯近似的可靠性结果,呈现出与$$的对应关系
\[\begin{align} \nonumber & 28\prec 15,\ 24\prec 11\Leftrightarrow \beta <1.221 \\ \nonumber & \ \ \ \ \ \ \ \ \ \ \ \ 14\prec 19\Leftrightarrow \beta <1.325 \\ \nonumber & \ \ \ \ \ \ \ \ \ \ \ \ 24\prec 13\Leftrightarrow \beta <1.272 \\ \end{align}\]
对于序\(\left\{ 7,24 \right\}\),虽然依赖于SNR的可靠性结果为\(7\succ 24\),但大量仿真结果表明\(7\prec 24\)具有更好的性能。因此选择
\[7\prec 24\Leftrightarrow \beta >1.179\]
此时,$\(的取值范围进一步缩小到\)( 1.179,1.221 )$。
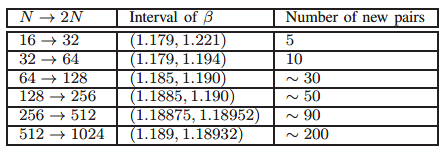
对于\(n>5\)(\(N>32\))的情况,继续重复这一搜索过程,得到如下表中所示的结果。随着\(N\)的增加,$$的取值范围不断缩小,并接近于\(1.1892\approx { {2}^{ {1}/{4}\;}}\)。新的序对小于合成信道总数的20%。
渐进性分析与数值仿真结果
β-expansion可以转化为贝努力卷积(Bernoulli
Convolution)概念。贝努力卷积定义了概率测度
\[{ {v}_{\lambda }}=\sum\limits_{i=1}^{+\infty }{ { {b}_{i}}}{ {\beta }^{i}}\]
假设\(B=\left( ...,{ {b}_{1}},{ {b}_{0}} \right)\)是二进制独立随机序列,满足
\[\Pr \left\{ { {b}_{i}}=1 \right\}=\Pr \left\{ { {b}_{i}}=0 \right\}=0.5,\forall i\]
测度\({ {v}_{\lambda }}\)要么是绝对连续的,要么是奇异的。我们需要的正是\({ {v}_{\lambda }}\)的绝对连续,使得在无限长的序列上能够进行全排列。令\(\beta ={ {2}^{ {1}/{k}\;}}\),已经证明当\(k=4\)时,即\(\beta \text{=}1.1892\)时,满足绝对连续的必要条件。这与上表中的观察一致。
图3则从仿真结果上表明β-expansion与高斯近似的性能相同。
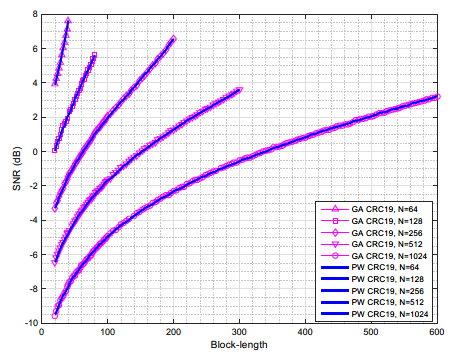
至此,从理论分析到仿真结果,充分论证了β-expansion算法的可行性和优越性。
参考文献
[1] C. Schurch, “A partial Order for the Synthesized Channels of
a Polar Code, ISIT 2016. [2] 3GPP, R1-167209, Polar code design and rate
matching, Huawei, HiSilicon. [3] β-expansion A Theoretical Framework for
Fast and Recursive Construction of Polar Codes, Huawei.