Polar Code(2)编码原理
前言
在《Polar
Code(1)概述》中建立了Polar Code初步印象,本文将详细阐述Polar
Code编码原理。Polar
Code是通过引入信道极化概念而构建的。信道极化分为两个阶段,分别是信道联合和信道分裂。通过信道的联合与分裂,各个子信道的对称容量将呈现两级分化的趋势:随着码长(也就是联合信道数)\(N\)的增加,一部分子信道的容量趋于1,而其余子信道的容量趋于0。Polar
Code正是利用这一信道极化的现象,在容量趋于1的\(K\)个子信道上传输消息比特,在其余子信道上传输冻结比特(即收发双方已知的固定比特,通常设置为全零)。由此构成的编码即为Polar
Code,码率为\({K}/{N}\;\)。
预备知识
一个二进制输入离散无记忆信道(B-DMC)可表示为\(W:X\to Y\),\(X\)是输入符号集合,\(Y\)是输出符号集合,转移概率为\(W\left( y|x \right),x\in X,y\in
Y\)。由于信道是二进制输入,集合\(X=\left\{ 0,1 \right\}\);\(Y\)和\(W\left(
y|x \right)\)是任意值。对信道\(W\)的\(N\)次使用后的信道可表示为\({W^{N}}\),则信道\({W^{N}}:{X^{N}}\to
{Y^{N}}\)的转移概率为\({W^{N}}\left(
y_1^{N}|x_{1}^{N} \right)=\prod\nolimits_{i=1}^{N}{W\left( y|x
\right)}\)。
对于一个B-DMC \(W\),有两个重要的信道参数:
对称容量(Symmetric Capacity)
\[I\left( W \right)\triangleq \sum\limits_{y\in Y}{\sum\limits_{x\in X}{\frac{1}{2}}}W\left( y|x \right)\log \frac{W\left( y|x \right)}{\frac{1}{2}W\left( y|0 \right)+\frac{1}{2}W\left( y|1 \right)}\]
巴氏参数(Bhattacharyya Parameter)
\[Z\left( W \right)\triangleq \sum\limits_{y\in Y}{\sqrt{W\left( y|0 \right)W\left( y|1 \right)}}\]
\(I\left( W \right)\)是对信道速率的度量,\(Z\left( W \right)\)对信道可靠性的度量。\(I\left( W \right)\)是信道\(W\)在等概率输入下的可靠传输时的最大速率;而\(Z\left( W \right)\)是信道\(W\)只传输0或1下的最大似然判决错误概率的上限。
\(I\left( W \right)\)与\(Z\left( W \right)\)的取值范围均为\(\left[ 0,1 \right]\)。由于对数以2为底,因此码率和信道容量的单位为bit。\(I\left( W \right)\)与\(Z\left( W \right)\)满足这样的关系:且仅当\(Z\left( W \right)\approx 0\)时,\(I\left( W \right)\approx 1\);当且仅当\(Z\left( W \right)\approx 1\)时,\(I\left( W \right)\approx 0\)。
当\(W\)为对称信道时,\(I\left( W \right)\)等于香农容量。所谓信道对称,即满足:对于任意\(y\in Y\),有\(W\left( y|0 \right)=W\left( -y|1 \right)\)。二进制对称信道(Binary Symmetric Channel,BSC)和二进制删除信道(Binary Erasure Channel,BEC)都是满足对称性的B-DMC。具体地说,对于\(Y=\left\{ 0,1 \right\}\),满足\(W\left( 0|0 \right)=W\left( 1|1 \right)\)且\(W\left( 1|0 \right)=W\left( 0|1 \right)\)的B-DMC是为BSC。对于\(y\in Y\),满足\(W\left( y|0 \right)W\left( y|1 \right)=0\)或\(W\left( y|0 \right)=W\left( y|1 \right)\)的B-DMC是为BEC。对于BEC,符号\(y\)称为删除符号(Erasure Symbol)。
行向量\(\left( {a_{1}},...,{a_{N}} \right)\)在这里简写为\(a_{1}^{N}\)。对于给定的行向量\(a_{1}^{N}\),其子向量表示为\(a_{i}^{j},1\le i,j\le N\),且\(i\le j\)。对于给定的\(a_{1}^{N}\)和\(A\subset \left\{ 1,...,N \right\}\),记\({a_{A}}\)表示子向量\(\left( {a_{i}}:i\in A \right)\)。记\(a_{1,o}^{j}\)表示奇数索引的子向量 \(\left( {a_{k}}:1\le k\le j;\begin{matrix} k & odd \\ \end{matrix} \right)\),记\(a_{1,e}^{j}\)表示偶数索引的子向量\(\left( {a_{k}}:1\le k\le j;\begin{matrix} k & even \\ \end{matrix} \right)\)。例如,对于向量\(a_{1}^{5}=\left( 5,4,6,2,1 \right)\),有\(a_{2}^{4}=\left( 4,6,2 \right)\),\(a_{1,e}^{5}=\left( 4,2 \right)\),\(a_{1,o}^{4}\left( 5,6 \right)\)。全零向量则记为\(0_{1}^{N}\)。
在此所讨论的向量、矩阵的运算均是在二元域上的运算,即GF(2)。记$\(为模2加,记\)\(为克罗内克积(Kronecker Power)。记\){A{n}}\(表示\)A\(的\)n\(次克罗内克积,有递归式\){A{n}}=A,n\(,并且定义\){A^{}}=$。
记\(\left| A \right|\)表示集合\(A\)中元素的个数。记\({1_{A}}\)表示集合\(A\)的指示函数,若\(x\in A\),则\({1_{A\left( x \right)}}=1\);若\(x\notin A\),则\({1_{A\left( x \right)}}=0\)。
信道极化
信道极化分为两个阶段:信道联合阶段(Channel
Combining)和信道分裂(Channel Splitting)阶段。
信道联合
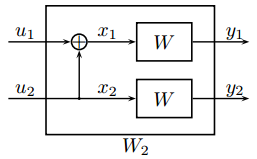
在这一阶段,联合B-DMC \(W\)的\(N\)个独立副本,通过递归方式产生一个向量信道\({W_{N}}:{X^{N}}\to {Y^{N}}\),其中\(N\)为2的幂次\(N={2^{n}},n\ge 0\)。递归开始于第0级(\(n=0\)),只使用\(W\)的1个副本,并定义\({W_{1}}\triangleq W\)。第1级(\(n=1\))递归联合了2个独立副本,如图1所示,得到向量信道\({W_{2}}:{X^{2}}\to
{Y^{2}}\),其转移概率为
\[{W_{2}}\left( {y_{1}},{y_{2}}|{u_{1}},{u_{2}} \right)=W\left( {y_{1}}|{u_{1}}\oplus {u_{2}} \right)W\left( {y_{2}}|{u_{2}} \right)\]
第2级(\(n=2\))递归如图2所示,联合信道\({W_{2}}\)的2个独立副本得到信道\({W_{4}}:{X^{4}}\to {Y^{4}}\),其转移概率为
\[{W_{4}}\left( y_{1}^{4}|u_{1}^{4} \right)={W_{2}}\left( y_{1}^{2}|{u_{1}}\oplus {u_{2}},{u_{3}}\oplus {u_{4}} \right){W_{2}}\left( y_{3}^{4}|{u_{2}},{u_{4}} \right)\]
在图2中,\({R_{4}}\)是完成从\(\left( {s_{1}},{s_{2}},{s_{3}},{s_{4}} \right)\)到\(v_{1}^{4}=\left( {s_{1}},{s_{3}},{s_{2}},{s_{4}} \right)\)的置换操作(排序)。从信道\({W_{4}}\)的输入\({W^{4}}\)的输入的映射\(u_{1}^{4}\to x_{1}^{4}\)可用公式表示为\(x_{1}^{4}=u_{1}^{4}{G_{4}}\),\({G_{4}}=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ \end{matrix} \right]\)。因此\({W_{4}}\)和\({W^{4}}\)的转移概率有关系式\({W_{4}}\left( y_{1}^{4}|u_{1}^{4} \right)={W^{4}}\left( y_{1}^{4}|u_{1}^{4}{G_{4}} \right)\)。
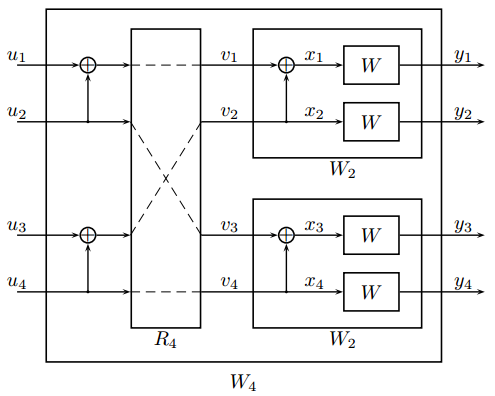
图3所示为递归结构的一般形式。\({W_{N/{2}\;}}\)的2个独立副本联合产生信道\({W_{N}}\)。输入向量\(u_{1}^{N}\)进入信道\({W_{N}}\),首先被转换为\(s_{1}^{N}\):\({s_{2i-1}}={u_{2i-1}}\oplus {u_{2i}}\),\({s_{2i}}={u_{2i}}\),\(1\le i\le {N}/{2}\;\)。\({R_{N}}\)表示比特反转排序操作,输入为\(s_{1}^{N}\),输出为\(v_{1}^{N}=\left( {s_{1}},{s_{3}},...,{s_{N-1}},{s_{2}},{s_{4}},...,{s_{N}} \right)\)。\(v_{1}^{N}\)则成为2个\({W_{N/{2}\;}}\)独立副本的输入。

映射\(u_{1}^{N}\to v_{1}^{N}\)是二元域GF(2)上的线性变换。\(u_{1}^{N}\to x_{1}^{N}\)是由复合信道\({W_{N}}\)的输入到原始信道\({W^{N}}\)的输入的映射,其映射过程也是线性变换。因此有\(x_{1}^{N}=u_{1}^{N}{G_{N}}\)。称\({G_{N}}\)为\(N\)维生成矩阵。信道\({W_{N}}\)和\({W^{N}}\)的转移概率有如下关系:
\[{W_{N}}\left( y_{1}^{N}|u_{1}^{N} \right)={W^{N}}\left( y_{1}^{N}|u_{1}^{N}{G_{N}} \right)\]
其中\(y_{1}^{N}\in {Y^{N}},u_{1}^{N}\in {X^{N}}\)。
信道分裂
这是信道极化的第二阶段。将信道联合构成的复合信道\({W_{N}}\)分裂为\(N\)个二进制输入的坐标信道(Coordinate
Channels)\(W_{N}^{\left( i \right)}:X\to
{Y^{N}}\times {X^{i-1}},1\le i\le N\),定义其转移概率为
\[W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|{u_{i}} \right)\triangleq \sum\limits_{u_{i+1}^{N}\in {X^{N-i}}}{\frac{1}{2^{N-1}}{W_{N}}\left( y_{1}^{N}|u_{1}^{N} \right)}\]
其中\(\left( y_{1}^{N},u_{1}^{i-1} \right)\)表示\(W_{N}^{\left( i \right)}\)的输出,而\({u_{i}}\)表示\(W_{N}^{\left( i \right)}\)的输入。
奇序分裂子信道和偶序分裂子信道的转移概率由两个递归式得到。对任何\(n\ge 0,N={2^{n}},1\le i\le {N}/{2}\;\),有
\[W_{N}^{\left( 2i-1 \right)}\left( y_{1}^{N},u_{1}^{2i-2}|{u_{2i-1}} \right)=\sum\limits_{u_{2i}}{\frac{1}{2}W_{N/{2}\;}^{\left( i \right)}\left( y_{1}^{N/{2}\;},u_{1,o}^{2i-2}\oplus u_{1,e}^{2i-2}|{u_{2i-1}}\oplus {u_{2i}} \right)\cdot W_{N/{2}\;}^{\left( i \right)}\left( y_{N/{2}\;+1}^{N},u_{1,e}^{2i-2}|{u_{2i}} \right)}\]
\[W_{N}^{\left( 2i \right)}\left( y_{1}^{N},u_{1}^{2i-1}|{u_{2i}} \right)=\frac{1}{2}W_{N/{2}\;}^{\left( i \right)}\left( y_{1}^{N/{2}\;},u_{1,o}^{2i-2}\oplus u_{1,e}^{2i-2}|{u_{2i-1}}\oplus {u_{2i}} \right)\cdot W_{N/{2}\;}^{\left( i \right)}\left( y_{N/{2}\;+1}^{N},u_{1,e}^{2i-2}|{u_{2i}} \right)\]
信道极化定理
定理1:对任意B-DMC \(W\)与任意\(\delta
\in \left( 0,1 \right)\),当\(N\)以2的幂次趋近于无穷大时,极化信道\(W_{N}^{\left( i \right)}\)中,满足\(I\left( W_{N}^{\left( i \right)} \right)\in \left(
1-\delta ,1 \right]\)的信道数占总信道数\(N\)的比例趋于\(I\left( W \right)\);满足\(I\left( W_{N}^{\left( i \right)} \right)\in \left[
0,\delta \right)\)的信道所占的比例趋于\(1-I\left( W \right)\)。
定理2:对任意B-DMC \(W\),\(I\left( W \right)>0\),且对任意\(R<I\left( W \right)\),存在一个序列集合\({A_{N}}\subset \left\{ 1,...,N \right\},N\in \left\{ 1,2,...,{2^{n}},... \right\}\),对所有\(i\in {A_{N}}\)有\(\left| {A_{N}} \right|\ge NR\)且\(Z\left( W_{N}^{\left( i \right)} \right)\le O\left( {N^{-5/{4}\;}} \right)\)。
极化编码
利用极化现象构建的编码可以达到对称容量\(I\left( W \right)\),称为极化编码(Polar
Coding)。极化编码的基本思想是:只在\(Z\left(
W_{N}^{\left( i \right)} \right)\)近于0的坐标信道\(W_{N}^{\left( i
\right)}\)上发送数据比特。极化码具有一般的二元线性分组码的基本编码要素,因而可以通过显示地写出其生成矩阵来完成编码:
\[x_{1}^{N}=u_{1}^{N}{G_{N}}\]
其中\(u_{1}^{N}\)为原始比特序列,\(x_{1}^{N}\)为编码后的比特序列,\({G_{N}}\)为生成矩阵,码长为\(N={2^{n}}\)。
极化编码步骤:
- 极化信道可靠性估计
- 比特混合
- 构造生成矩阵
极化信道可靠性估计
对于BEC,Arikan给出的方法是计算巴氏参数
\[Z\left( W_{N}^{\left( i \right)} \right)=\sum\limits_{y_{1}^{N}\in {Y^{N}}}{\sum\limits_{u_{1}^{i-1}\in {X^{i-1}}}{\sqrt{W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|0 \right)W_{N}^{\left( i \right)}\left( y_{1}^{N},u_{1}^{i-1}|1 \right)}}}\]
\(Z\left( W_{N}^{\left( i \right)} \right)\)越小,相应的对称容量\(I\left( W_{N}^{\left( i \right)} \right)\)越大;反之,\(Z\left( W_{N}^{\left( i \right)} \right)\)越大,说明该信道越不可靠。
对于非BEC,如BSC信道或AWGNC,不能得到精确的巴氏参数,需要采用密度进化或高斯近似法估计信道的可靠性,详见《Polar Code(4)编码之极化信道可靠性估计》。
比特混合
在这一步的规则是:选择可靠性最大的\(K\)个分裂子信道传输消息比特,其他分裂子信道传输冻结比特。这一步的输出即为编码的原始比特\(u_{1}^{N}\)。
对于BEC来说,选择巴氏参数最小的\(K\)个子信道放置消息比特。
构造生成矩阵
生成矩阵表示为
\[{G_{N}}\text{=}{B_{N}}{F^{\otimes n}}\]
其中\({F^{\otimes n}}\)表示对矩阵\(F=\left[ \begin{matrix} 1 & 0 \\ 1 & 1 \\ \end{matrix} \right]\)的\(n\)次克罗内克积,有递归式\({F^{\otimes n}}\text{=}F\otimes {F^{\otimes \left( n-1 \right)}}\)。\({B_{N}}\)是排序矩阵,用以完成比特反序重排操作。所有比特反序重排,就是将每个原序列的十进制序号\(i\in \left\{ 1,2,...,N \right\}\)按二进制表示为\(\left( i-1 \right)\to \left( {b_{n}},{b_{n-1}},...,{b_{1}} \right)\),其中\({b_{n}}\)为最高有效位;再将该二进制序列反序,得到\(\left( {b_{1}},{b_{2}},...,{b_{n}} \right)\);最后以\({b_{1}}\)为最高有效位重新按十进制表示成\(\left( {b_{1}},{b_{2}},...,{b_{n}} \right)\to \left( j-1 \right)\),令输出序列的第\(j\)个元素取值为原序列的第\(i\)个元素。\({B_{N}}\)的递归式定义为
\[{B_{N}}={R_{N}}\left( {I_{2}}\otimes {B_{N/{2}\;}} \right)\]
其中\({I_{2}}\)为2维单位阵,\({B_{2}}={I_{2}}\);矩阵\({R_{N}}\)为置换矩阵,对输入序列完成奇序元素和偶序元素的分离,即先排奇序元素,再排偶序元素,其作为效果如下
\[\left( {u_{1}},{u_{2}},{u_{3}},{u_{4}},...,u{}_{N} \right)\times {R_{N}}=\left( {u_{1}},{u_{3}},{u_{5}},...,{u_{N-1}},{u_{2}},{u_{4}},{u_{6}},...,{u_{N}} \right)\]
总结
本文首先介绍了Polar
Code的预备知识,如对称容量、巴氏参数以及所涉及的数学符号的表示。其次介绍了信道极化的两个阶段:信道联合与信道分裂。最后阐述了Polar
Code的编码过程:通过构造生成矩阵获得\({G_{N}}\),通过计算各个分裂子信道的错误概率用以判断消息比特位置从而获得\(u_{1}^{N}\);两者相乘\(u_{1}^{N}{G_{N}}\)即为Polar Code。
极化码是一种线性分组码,通过构造生成矩阵而获得编码。只要给定码长\(N\),编译码结构就唯一确定。极化码基于信道极化现象,做到了扬长而避短。在最可靠的子信道上传输消息比特是为扬长,在最不可靠的子信道上传输冻结比特是为避短。
参考文献
[1] Arikan E. Channel Polarization: A Method for Constructing
Capacity-Achieving Codes for Symmetric Binary-Input Memoryless
Channels[J]. IEEE Transactions on Information Theory, 2008,
55(7):3051-3073.