Polar Code(19)当我们谈论design-snr时我们在谈论什么
前言
本文对论文“A Comparative Study of Polar Code Constructions for
the AWGN Channel”进行解读。
极化码构造
论文首先锁定了讨论的范围是极化码构造。极化码是线性分组码,极化码的码长N一旦确定,其生成矩阵随之确定;此时,比特信道的选择就完全地定义了一个极化码,不同的比特信道位置,其对应的编码结果不同。因此将比特信道的选择过程称为“极化码构造”(polar
code construction)。
极化码构造对于有限码长的最佳性能至关重要。极化码的构造在理论上有明确地定义,无非是从N个比特信道中选择最可靠的K个子信道。但现实的挑战是,你怎么知道哪些子信道是最可靠的?——极化信道的可靠性估计。于是引出了许多估计方法,如巴氏参数界法、蒙特卡洛估计法、TPM估计法、高斯近似法。
design-snr
极化码有个重要特性就是它的非普遍性(non-universality)。不同的极化码在给定的不同SNR下是不同的。实际的无线信道,其SNR是可能变化的。但我们不希望编码总是跟着信道SNR变化。因此我们希望有一个“一劳永逸”的解决方案,只设定一个SNR值,让它能够适用于一定范围内变化的SNR。这个SNR值被称为design-snr。
那么design-snr值究竟是多少呢?它等于多少时才使极化码性能达到最优呢?能够使极化码性能最优的design-snr就是the best design-snr。本论文的目的,就是找到the best design-snr。
作者指出极化码性能取决于三个因素,码率、码长和码构造算法。这意味着不同的码率、不同的码长、不同的码构造算法,the best design-snr也可能不同。再进一步明确本论文的目的,在规定的码率和码长(R=0.5,N=2048)下,分别找到不同码构造算法对应的最优design-snr。
the best design-snr
怎么找?作者给出了一个搜索算法,其实就是试数法。假如我们感兴趣的SNR范围是{S1,S2,…,Sm}。令design-snr依次取每一个Si值,看看在哪个Si下,对应的码构造算法性能最优。使性能最优的那个Si值就是我们要找的the
best design-snr。
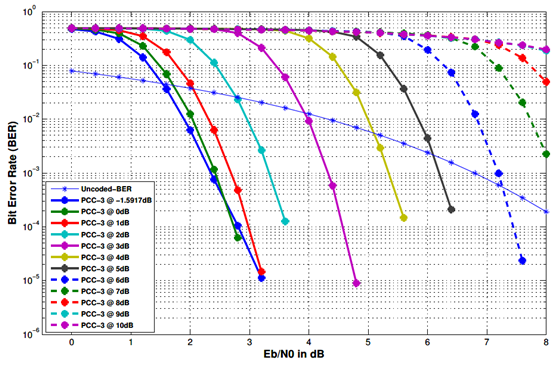
如上图所示,高斯近似法在N=2048,R=0.5的条件下,性能最好的是那条蓝色实线,其对应的design-snr=-1.5917dB。这就是要找的the best design-snr。
也就是说,在感兴趣的SNR={-1.5917,0,1,2,…,10}dB中,使高斯近似法性能达到最优的design-snr=-1.5917dB。So, -1.5917 dB is the best design-snr for GA.
反过来看,这个最佳design-snr对大多范围内的SNR有效呢?上图的横坐标是EbN0,纵坐标是BER。如果要使BER性能达到10-3以下,在给定最佳design-snr下,EbN0大约只需2.4dB。
对需要满足的BER性能指标,所需EbN0越小越好。而众多感兴趣的SNR值中,只有在最佳design-snr下,所需EbN0是最小的。换句话说,如果所用的 design-snr不是最佳design-snr,要满足一定的BER性能,所需要的EbN0就要更大一些,这意味着对信道条件的要求更苛刻一些。
\(SNR=\frac{ { {E}_{s}}}{ { {N}_{0}}}=R\cdot \frac{ { {E}_{b}}}{ { {N}_{0}}}\)
写成dB形成:
\(SNR\left( dB \right)=EbN0\left( dB \right)+10\log 10\left( R \right)\)
\(SNR\left( dB \right)=2.4+10\log 10\left( 0.5 \right)=-0.6dB\)
也就是说,对于高斯近似法,在最佳design-snr=-1.5917dB下,要达到BER=10-3的性能,所需SNR只要-0.6dB。换言之,对于高斯近似法,要达到BER=10-3的性能,对于N=2048,R=0.5,只要信道SNR大于-0.6dB,这个最佳design-snr值就是适用的。
如此看来,design-snr意义非凡。
参考文献
[1] Vangala H, Viterbo E, Hong Y. A comparative study of polar
code constructions for the AWGN channel[J]. arXiv preprint
arXiv:1501.02473, 2015.