Polar Code(12)B-DMC对称容量
前言
任何一本信息论书籍讲到离散信道容量时都会涉及形如\(I\left( X;Y \right)=\sum\limits_{i,j}{ { {p}_{i}}{
{p}_{ij}}\log \frac{ { {p}_{ij}}}{ {
{q}_{j}}}}\)的公式。但这个公式,我理解是经过转化得来的,不是直接得到的。怎么转化呢?请继续阅读。
输入符号概率\({ {p}_{i}}=p\left( { {x}_{i}} \right)\),输出符号概率\({ {q}_{j}}=q\left( { {y}_{j}} \right)\),输入符号到输出符号的转移概率\({ {p}_{ij}}=p\left( { {y}_{j}}|{ {x}_{i}} \right)\),这三种概率完全地表达了一个信道。对于信道容量,第一个概念是互信息量。
互信息量
互信息量定义为后验概率与先验概率比值的对数。虽然有这个定义,但必须先要明确观察者的角度才能进一步确定后验概率是谁,先验概率是谁。\(I\left( X;Y
\right)\)是站在接收端的角度观察,是\(Y\)对\(X\)的平均互信息量;而\(I\left( Y;X
\right)\)是站在发送端角度观察,是\(X\)对\(Y\)的平均互信息量。我们只说第一种角度,即以接收者的视角来观察信道。
通常接收端可以预知信息\(X\)发出的各个符号的集合,以及它们的概率分布,也就是说发送符号概率\(p\left( { {x}_{i}} \right)\)是先验概率。当接收端收到一个符号\({ {y}_{j}}\)后,接收端可以计算发送端消息的条件概率\(p\left( { {x}_{i}}|{ {y}_{j}} \right)\),这种条件概率就是后验概率。根据互信息量定义,\({ {y}_{j}}\)对\({ {x}_{i}}\)的互信息量为:
\[\begin{align} I\left( { {x}_{i}};{ {y}_{j}} \right)=\log \frac{p\left( { {x}_{i}}|{ {y}_{j}} \right)}{p\left( { {x}_{i}} \right)} \end{align}\]
平均互信息量
只有\(I\left( { {x}_{i}};{ {y}_{j}}
\right)\)是没有意义的,因为通常无法确定\(p\left( { {x}_{i}}|{ {y}_{j}}
\right)\)和\(p\left( { {x}_{i}}
\right)\)的大小关系,\(I\left( {
{x}_{i}};{ {y}_{j}} \right)\)不一定大于或等于0。由于发送符号\(X\)和接收符号\(Y\)都是随机变量,要探知\(Y\)对\(X\)的互信息量得用统计的方法去计算\(I\left( { {x}_{i}};{ {y}_{j}}
\right)\)的平均值,准确地说是计算\(I\left( { {x}_{i}};{ {y}_{j}}
\right)\)在发送符号集合\(X\)和接收符号集合\(Y\)上的概率加权统计平均值,这就是平均互信息量:
\[\begin{align} I\left( X;Y \right)=\sum\limits_{i}{\sum\limits_{j}{p\left( { {x}_{i}}{ {y}_{j}} \right)}\log }\frac{p\left( { {x}_{i}}|{ {y}_{j}} \right)}{p\left( { {x}_{i}} \right)} \end{align}\]
其中\(p\left( { {x}_{i}}{ {y}_{j}} \right)\)是发送符号\({ {x}_{i}}\)与接收符号\({ {y}_{j}}\)的联合概率。
联合概率、后验概率与转移概率的关系
\[\begin{align} p\left( { {x}_{i}}{ {y}_{j}} \right)=p\left( { {x}_{i}} \right)p\left( { {y}_{j}}|{ {x}_{i}} \right)=p\left( { {y}_{j}} \right)p\left( { {x}_{i}}|{ {y}_{j}} \right) \end{align}\]
这个关系式相当重要!它打通了前向与后向之间的联系。
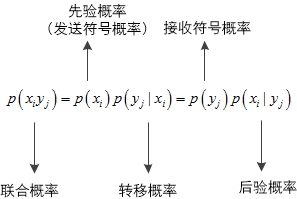
研究互信息量自然离不开对信道的定义。而信道是由输入符号、输出符号和转移概率三者确定的。转移概率\(p\left( { {y}_{j}}|{ {x}_{i}} \right)\)是站在发送端的角度观察,方向是\(X\to Y\),因此也称为前向概率。后验概率\(p\left( { {x}_{i}}|{ {y}_{j}} \right)\)是站在接收端的角度观察,方向是\(Y\to X\),因此也称为后向概率。后验概率是逆向思维,不仅难以理解而且还不易求,既然如此那就全部按正向来吧。根据关系式(3),把后验概率用转移概率来表示:
\[\begin{align} p\left( { {x}_{i}}|{ {y}_{j}} \right)=\frac{p\left( { {x}_{i}} \right)p\left( { {y}_{j}}|{ {x}_{i}} \right)}{p\left( { {y}_{j}} \right)} \end{align}\]
带入式(2)则平均互信息量\(I\left( X;Y \right)\)用转移概率可重新表示为:
\[\begin{align} I\left( X;Y \right)=\sum\limits_{i}{\sum\limits_{j}{p\left( { {x}_{i}} \right)p\left( { {y}_{j}}|{ {x}_{i}} \right)}\log }\frac{p\left( { {y}_{j}}|{ {x}_{i}} \right)}{p\left( { {y}_{j}} \right)} \end{align}\]
其中\(p\left( { {x}_{i}} \right)\)是先验概率自不必说,\(p\left( { {y}_{j}} \right)\)是接收符号概率也可以用转移概率表示:
\[\begin{align} p\left( { {y}_{j}} \right)=\sum\limits_{i}{p\left( { {x}_{i}} \right)}p\left( { {y}_{j}}|{ {x}_{i}} \right) \end{align}\]
通过式(5~6)可以看出,在信道给定的情况下,平均互信息量\(I\left( X;Y \right)\)的大小由输入符号的概率分布\(p\left( { {x}_{i}} \right)\)来确定。
信道容量
进一步,信道容量定义为平均互信息量\(I\left( X;Y \right)\)的最大值,用符号\(C\)来表示,即
\[\begin{align} C=\underset{p\left( { {x}_{i}} \right)}{\mathop{\max }}\,I\left( X;Y \right)=\underset{p\left( { {x}_{i}} \right)}{\mathop{\max }}\,\sum\limits_{i}{\sum\limits_{j}{p\left( { {x}_{i}} \right)p\left( { {y}_{j}}|{ {x}_{i}} \right)}\log }\frac{p\left( { {y}_{j}}|{ {x}_{i}} \right)}{\sum\limits_{i}{p\left( { {x}_{i}} \right)}p\left( { {y}_{j}}|{ {x}_{i}} \right)} \end{align}\]
什么时候\(I\left( X;Y \right)\)取得最大值呢?根据信息论,在对称信道下,输入等概时互信息量达到最大值,该最大值即为信道容量\(C\)。在非对称信道下,也一定存在某种输入概率分布,使得互信息量\(I\left( X;Y \right)\)最大,该最大值即为该信道的容量,而相应的输入概率分布称为最佳输入分布。当信道给定后,转移概率\(p\left( { {y}_{j}}|{ {x}_{i}} \right)\)就固定,\(C\)仅与\(p\left( { {y}_{j}}|{ {x}_{i}} \right)\)有关,而与\(p\left( { {x}_{i}} \right)\)无关。
B-DMC平均互信息量
对于一般二进制离散无记忆信道(此时先不论信道是否对称),假定信源符号以等概率发送,则有\(p\left( 0 \right)=p\left( 1
\right)=\frac{1}{2}\),带入式(2)得到输入等概时的平均互信息量:
\[\begin{align} I\left( X;Y \right)=\sum\limits_{i}{\sum\limits_{j}{\frac{1}{2}p\left( { {y}_{j}}|{ {x}_{i}} \right)}\log }\frac{p\left( { {y}_{j}}|{ {x}_{i}} \right)}{\sum\limits_{i}{p\left( { {x}_{i}} \right)}p\left( { {y}_{j}}|{ {x}_{i}} \right)} \end{align}\]
分母展开\(\sum\limits_{i}{p\left( { {x}_{i}} \right)}p\left( { {y}_{j}}|{ {x}_{i}} \right)=\frac{1}{2}p\left( { {y}_{j}}|0 \right)+\frac{1}{2}p\left( { {y}_{j}}|1 \right)\),并带入式(8)得到一般B-DMC在输入等概时的平均互信息量为:
\[\begin{align} I\left( X;Y \right)=\sum\limits_{i}{\sum\limits_{j}{\frac{1}{2}p\left( { {y}_{j}}|{ {x}_{i}} \right)}\log \frac{p\left( { {y}_{j}}|{ {x}_{i}} \right)}{\frac{1}{2}p\left( { {y}_{j}}|0 \right)+\frac{1}{2}p\left( { {y}_{j}}|1 \right)}} \end{align}\]
由于此时还未定义这个一般B-DMC是否为对称信道,虽然假定输入等概,但此时不能确定(9)式的最大值。下面添加对称性条件。
对称信道容量
如果转移概率矩阵\(\mathbf{P}\)的每一行都是第一行的置换,称该矩阵是输入对称的;如果转移概率矩阵\(\mathbf{P}\)的每一列都是第一列的置换,称该矩阵是输出对称的;如果输入、输出都对称,则称该DMC为对称的DMC信道。
满足对称条件的B-DMC有两个典型例子:BSC和BEC。其中BSC的转移概率矩阵为
\[\begin{align} \mathbf{P}=\left[ \begin{matrix} p & 1-p \\ 1-p & p \\ \end{matrix} \right] \end{align}\]
显然式(10)的每一行、每一列都分别是第一行、第一列的置换,因此转移概率满足式(10)的信道是一种对称信道。把BSC转移概率带入式(9)得到平均互信息量
\[\begin{align} I\left( X;Y \right)=p\log 2p+\left( 1-p \right)\log 2\left( 1-p \right) \end{align}\]
此时的平均互信息量就是所能达到的最大值,因为式(11)是输入等概下的对称信道的平均互信息量,即对称信道的容量,也即BSC的对称容量。此时才有
\[\begin{align} C=I\left( X;Y \right)=p\log 2p+\left( 1-p \right)\log 2\left( 1-p \right) \end{align}\]
理解
既然是离散信道,其输入、输出必然都是离散的。为什么输出符号是任意的?站在发送端的角度去看,发送端唯一确知的就是自己能够发什么,发送符号取值范围是{0,1},这是明确的。我发的信号我做主,发送端只管得了自己,但它不并知道信道是什么样的,也不知道接收端能收到什么。所以对于发送端而言,信道和接收符号都是未知的、任意的。概率也仅仅表达了一种可能性。弓箭手射箭,一旦射出,箭就不由弓箭手所控制了。
为什么Arikan由B-DMC直接给出了对称容量?式(9)给出的就是一般B-DMC的平均互信息量,此时还没涉及对称的概念。注意,式(9)是一个不完整的计算式,它有4个转移概率值仍是未知的。因此你必须对B-DMC有进一步的定义,而此时式(9)的值则完全取决于信道类型。转移概率满足什么样的特性,它就定义了什么样的信道类型。当满足\(P\left( 0|0 \right)=P\left( 1|1 \right)=p\)、\(P\left( 1|0 \right)=P\left( 0|1 \right)=1-p\)时,B-DMC就是BSC信道。对称,发0的情况和发1的情况完全相同,这就是对称。BSC是研究二元编解码最简单,最常用的信道模型。
研究编解码离不开具体的信道模型,只谈B-DMC是不够的,它还有4个概率值需要进一步给出定义。当进一步研究编码时不可能凭空讨论,一定要更加具体,是B-DMC下的BSC,还是B-DMC下的BEC?如此这般才构成讨论的基础。为什么一定要对称?因为它是最简单最基础的模型。定义就是定义,不需要纠结于为什么要这么定义。一上来就给出讨论的前提,在这种定义的框架下去讨论编码问题。
说“BSC的对称容量”、“BEC的对称容量”都没问题,因为BSC和BEC都是对称信道。说“B-DMC的对称容量”,其实是隐含地指出了B-DMC满足对称性,要么是BSC,要么是BEC。
BSC和BEC的相关链接: